Question
Question: In how many ways letters of the word ‘Monday’ can be written around a circle, if vowels are to be se...
In how many ways letters of the word ‘Monday’ can be written around a circle, if vowels are to be separated in any arrangement?
Solution
The above given question is of the permutation and combination. Permutation and combination are the ways to represent a group of objects by selecting them in a set and forming subsets. Actually it defines the various ways to arrange a certain group of data. When we select the objects from a certain group then it is said to be permutations where order matters, whereas the combination is a way of selecting items from a collection where order of selection does not matter.
Complete step by step solution:
The given word is ‘MONDAY’ and we have to arrange its letters around a circle with a condition that vowels are to be separated.
The total number of letters in the given word is6. Since, we have to separate vowels from the given word. We have to find the total number of vowels in the given word, which is 2 as A and O. It means we have to arrange only 6−2=4 words around the circle like
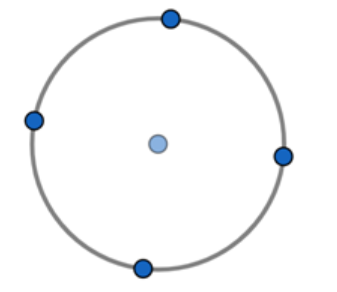
The total number of arrangements of the word ‘MONDAY’ is (6−1)!.Because it is a circular formation and the first and last terms will be close to each other so we subtract 1 from the total number of terms and find its factorial. Here factorial (!) means it multiplies a number by every number below it.
Here 5!=6×5×4×3×2×1 which further equals 5!=120.
Since we have to keep vowels separate then we will first find the number of ways in which vowels can be together and subtract it from total.
So we consider both “a” and “o” as single letters and write it as MNDYAO and find its number of arrangements. Which will be (5−1)!=4×3×2×1=24
Now subtract it from original value
So, the total arrangement of the given word is:
⇒120−24=96
Hence there are 96 arrangement of given word around a circle.
Note: When we have to arrange digits in a circular formation, we should always subtract one from the total elements of the word. In probability questions students get confused in solving the question. Actually to solve the probabilities question there are many rules which we have to remember.
