Question

In how many ways is it possible to choose a white square and a black square on a chessboard, so that squares must not lie in the same row or column?
A) $56$
B) $896$
C) $60$
D) $768$

Answer 1

Here, we use the method of combination to find ways to choose white and black squares. After choosing one square(be it black or white) we exclude the row and column common to that square so we avoid the situation where squares must not lie in one row or column and find ways to choose the second square from the remaining number of squares.

• A chess board contains an equal number of black and white squares and equal number or rows and columns as well.
• Combination is used when we have to find ways to choose without keeping in mind the order.

Complete step by step solution:
We know a chessboard has $8$ rows and $8$ columns, therefore total number of squares in a chessboard is $8 \times 8 = 64$
Since, there are equal numbers of white and black squares on a chessboard, therefore, number of white squares $= \dfrac{{64}}{2} = 32$
Number of black squares $= 32$

We have to choose one white square out of $32$ white squares.
Therefore ways to choose $1$ white square out of $32$ white squares is given by a combination formula
$^n{C_r} = \dfrac{{n!}}{{(n - r)!r!}}$
Where $n$ is the total number of white squares from which we choose and $r$ is the number of squares we have to choose from total white squares. Substituting the value of $n = 32,r = 1$ in the formula of combination
$^{32}{C_1} = \dfrac{{32!}}{{(32 - 1)! \times 1!}}$
$^{32}{C_1} = \dfrac{{32!}}{{31! \times 1!}}$
Now from the definition of factorial of a number $p! = p(p - 1)!$
Therefore, $32! = 32 \times 32!$ and $1! = 1$
$^{32}{C_1} = \dfrac{{32 \times 31!}}{{31!}}$
Cancelling out the same terms from both numerator and denominator.
$^{32}{C_1} = 32$ $...(i)$
Now after we choose one white square, we exclude that one row and that one column which gives us that one white square.

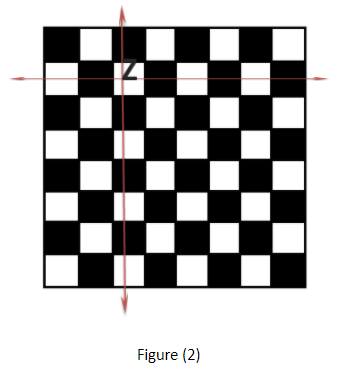
In figure (2), we select a white square denoted by Z , then we cancel out one row and one column.
Now we have to choose one black square .
Number of squares we have to choose from the board is now $8$ less than $32$ because $4$ black squares are cancelled out from that row and other $4$ black squares are cancelled out from that one column.
Therefore, $n = 32 - 8 = 24$ and $r = 1$
Number of ways to choose one black square from the remaining squares is given by
$^{24}{C_1} = \dfrac{{24!}}{{(24 - 1)! \times 1!}}$
$^{24}{C_1} = \dfrac{{24!}}{{23! \times 1!}}$
Now from the definition of factorial of a number $p! = p(p - 1)!$
Therefore, $24! = 24 \times 23!$ and $1! = 1$
$^{24}{C_1} = \dfrac{{24 \times 23!}}{{23!}}$
Cancelling out the same terms from both numerator and denominator.
$^{24}{C_1} = 24$ $...(ii)$
Total number of ways to choose one white square and one black square in such a way that squares must not lie in the same row or column is
$^{32}{C_1}{ \times ^{24}}{C_2}$
From equation $(i)$ and equation $(ii)$
$^{32}{C_1}{ \times ^{24}}{C_1} = 32 \times 24 = 768$

Therefore, option D is correct.

Note:
Students are likely to make mistakes while choosing the second square as it involves deduction of a row and a column. Attempting to calculate all the possibilities without the combination formula is a very long procedure which will take a lot of time as we will have to calculate each square separately, so it should be avoided.