Solveeit Logo
Login

Question

Question: In how many ways four men and three women may sit around a round table if all the women i) Always ...

In how many ways four men and three women may sit around a round table if all the women
i) Always sit together
ii) Never sit together

Explanation

Solution

There are a total of seven people from which 44 are men and 33 are women.

  1. For the women to always sit together around the round table, consider all the 33 women to be one group then total persons are 55 in number so use the formula the circular permutation of n different things is (n−1)!\left( {n - 1} \right)! to calculate the arrangement and arrangement of the women themselves can be in 3!3! ways.
  2. Since the total number of persons is 77 which can be arranged in 6!6! ways because the circular permutation of n different things is (n−1)!\left( {n - 1} \right)!. And then subtract the value obtained in i) from this to get the number of ways the four men and three women sit around a round table in which the women always sit together.

Complete step by step solution:
We have to find the total number of ways the men and women sit around the round table so that the women are always together.
Consider the three women be one group then total persons are 55 in number
And we know that the circular permutation of n different things is(n−1)!\left( {n - 1} \right)!.
So on using this we get,
The number of ways the five person can sit=(5−1)!=4!\left( {5 - 1} \right)! = 4!
Since the group of women consists of three women, the women themselves can interchange with themselves. So the number of ways the 33women can be arranged is 3!3!
Then,
⇒\Rightarrow The total number of ways the men and women sit around the round table so that the women are always together=number of ways the 55 person can sit× number of ways the 33women can be arranged
On putting the given values we get,
⇒\Rightarrow The total number of ways the men and women sit around the round table so that the women are always together =4!×3!4! \times 3!
We know n!=n×(n−1)!×...3,2,1n! = n \times \left( {n - 1} \right)! \times ...3,2,1
⇒\Rightarrow The total number of ways the men and women sit around the round table so that the women are always together = 4×3×2×1×3×2×14 \times 3 \times 2 \times 1 \times 3 \times 2 \times 1
On multiplying all the numbers we get,
⇒\Rightarrow The total number of ways the men and women sit around the round table so that the women are always together = 24×6=14424 \times 6 = 144
Answer-Hence the number of ways the men and women sit around the round table so that the women are always together=144144
ii) We have to find the total number of ways the men and women sit around the round table so that the women are never together.
So first we will find the total number of ways the 77 person can sit around a round table.
We know that the circular permutation of n different things is(n−1)!\left( {n - 1} \right)!.
So on using this we get,
The number of ways the seven person can sit=(7−1)!=6!\left( {7 - 1} \right)! = 6!
We know n!=n×(n−1)!×...3,2,1n! = n \times \left( {n - 1} \right)! \times ...3,2,1
Then the number of ways the seven person can sit=6×5×4×3×2×1=7206 \times 5 \times 4 \times 3 \times 2 \times 1 = 720
Now the total number of ways the men and women sit around the round table so that the women are never together= total number of ways the 77 person can sit around a round table−- total number of ways the men and women sit around the round table so that the women are always together.
So on putting the given values we get,
The total number of ways the men and women sit around the round table so that the women are never together=720−144=576720 - 144 = 576
Answer-the total number of ways the men and women sit around the round table so that the women are never together=576576

Note:
Here we can also solve the ii) by this method-
Consider the following arrangement-

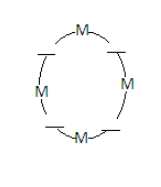
The spaces between the men are for the women so that no women can sit together. Since there are 44 men so they can be arranged in 4!4! ways.
There are44 spaces given for 33 women so the number of ways the three women can be arranged in those four spaces=4P3{}^4{P_3}
We knownPr=n!n−r!{}^n{P_r} = \dfrac{{n!}}{{n - r!}} . Son using this we get,
The number of ways the three women can be arranged in those four spaces=4!4−3!=4!\dfrac{{4!}}{{4 - 3!}} = 4!
Then the total number of ways the men and women sit around the round table so that the women are never together=4!×4!4! \times 4!
On using formulan!=n×(n−1)!×...3,2,1n! = n \times \left( {n - 1} \right)! \times ...3,2,1
The total number of ways the men and women sit around the round table so that the women are never together=4×3×2×4×3×2=5764 \times 3 \times 2 \times 4 \times 3 \times 2 = 576