Question

In how many different ways can five boys and five girls form a circle such that the boys and girls alternate?

Answer 1

Hint – In this particular type of question use the concept that as there are an equal number of boys and girls so first arrange any of them first on the circle then arrange the girls between them so use these concepts to reach the solution of the question.

Complete step-by-step answer:

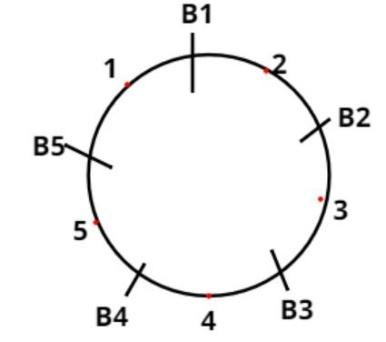
There are 5 boys and 5 girls.
Now we have to arrange them in a circle such that boys and girls alternate.
So first arrange the boys or the girls in a circle whichever is higher.
So as there are equal numbers of boys and girls so arrange any of these first.
Let us assume we arrange boys first.
So as we know that the number of possible arrangements of n boys in a circle is given as (n – 1)!
So the number of possible arrangements of 5 boys in a circle is given as (5 – 1)! = 4!
Now there are 5 places between them as shown in the figure so we have to arrange the girls in these places such that boys and girls are alternate.
So the number of possible arrangements of the girls are = 5!
So the total number of possible arrangements such that boys and girls are alternate = number of arrangements of boys in a circle multiplied by the number of arrangements of girls between the boys.
So the total number of possible arrangements such that boys and girls are alternate are, N = $4! \times 5!$
Now simplify this we have,
$\Rightarrow N = 4.3.2.1.5.4.3.2.1 = 24\left( {120} \right) = 2880$
So this is the required possible number of arrangements such that boys and girls are alternate.
So this is the required answer.

Note – Whenever we face such types of questions the key concept we have to remember is that we always recall that in a circular arrangement the number of possible arrangements of n objects in a circle is given as (n – 1)! So first find out the number of arrangements of the boys as above then arrange the girls in between them as above then multiply these two values and simplify, we will get the required answer.