Question

In gaseous reactions important for the understanding of the upper atmosphere $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ and O react by molecularly to form two $\text{ OH }$ radicals. $\text{ }\Delta \text{H }$ for this reaction is $\text{72 kJ }$ at 500 K and Ea is $\text{ 77 kJ mo}{{\text{l}}^{-1}}\text{ }$ , then Ea for the bimolecular recombination of two $\text{ OH }$ radicals to form $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ and O is:
A) $\text{ 3 kJ mo}{{\text{l}}^{-1}}$
B) $\text{ 4 kJ mo}{{\text{l}}^{-1}}$
C) $\text{ 5 kJ mo}{{\text{l}}^{-1}}$
D) $\text{ 7 kJ mo}{{\text{l}}^{-1}}$

Answer 1

The reaction to convert to the reactant or product either absorbs the heat or liberates the heat. The reaction in which the reactant liberates heat and forms reactant is exothermic. The reactant is converted into the product only when the molecules acquire the minimum energy to cross the energy barrier, activation energy Ea. On plot of potential energy against the reaction coordinates, for exothermic reactions the energy of the reactant is always on the high end as compared to the product. Activation energy for the backward reaction can be calculated as,
$\text{ E}{{\text{a}}_{\text{(Backward)}}}\text{ = E}{{\text{a}}_{\text{(forward)}}}\text{ + }\Delta {{\text{H}}_{\text{(exothermic)}}}$

Complete answer:
Here we have given the following data:
In the gaseous state, the $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ and O reacts by molecularly.i.e. The rate of reaction depends on the concentration of $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ and O and generates the $\text{ OH }$ radical.
The enthalpy of reaction is equal to $\text{ }\Delta \text{H= - 72 kJ }$
The activation energy of the reaction is,$\text{ Ea = 77 kJ mo}{{\text{l}}^{-1}}\text{ }$
We are interested to find out the activation energy for the recombination of two $\text{ OH }$ radicals to form $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ and O as the product.
The reactions of formation of $\text{ OH }$ radical (forward) are shown below,
$\text{ }{{\text{H}}_{\text{2}}}\text{O + O }\to \text{ 2O}{{\text{H}}^{\bullet }}\text{ }, \Delta \text{H = }-72\text{ kJ , Ea = 77 kJ mo}{{\text{l}}^{-1}}\text{ }$
The reactions of formation of $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ an O as the product from the two $\text{ OH }$ radical is given as follows,
$\text{ 2O}{{\text{H}}^{\bullet }}\text{ }\to \text{ }{{\text{H}}_{\text{2}}}\text{O + O }$
To find out the activation energy we must consider the plot of potential energy against the reaction coordinates.
Here, the forward reaction is forming a single product that liberates the energy thus the enthalpy of the reaction is negative. It means that reactant $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ and O initially placed at the high heat as shown in the figure. As the reaction proceeds the $\text{ }{{\text{H}}_{\text{2}}}\text{O}$ and O acquires the energy which is equal to the activation energy (or energy barrier) and transforms into the product. The $\text{ OH }$ radical formation is accompanied by the liberation of heat equal to the sum of enthalpy $\text{ }\Delta \text{H= + 72 kJ }$and activation energy .thus, the product have are stable and have low potential energy. This is summarised in the figure below,

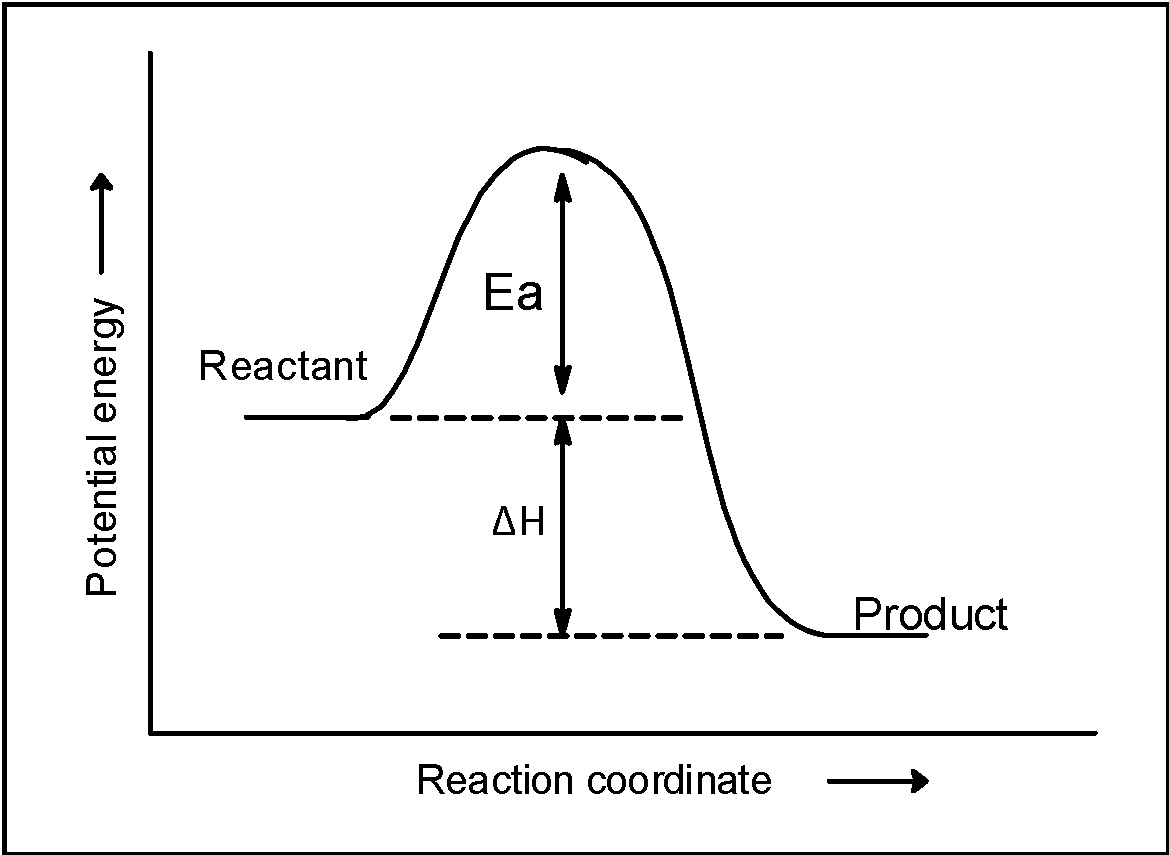
Now, from the plot, it is clear that if the product $\text{ OH }$ radical combines and goes towards the reactant then the activation energy acquired by the molecules must be equal to the sum of the activation energy of forwarding reaction and the enthalpy of reaction. This can be utilized to find the activation energy of backward reaction as follows,
$\text{ Ea }$ For the reverse reaction,
$\begin{aligned} & \text{ = E}{{\text{a}}_{\text{(forward)}}}\text{ + }\Delta \text{H } \\\ & \text{= 77 + (}-72) \\\ & \therefore \text{E}{{\text{a}}_{\text{(Backward)}}}\text{ = }~~+5\text{ kJ mo}{{\text{l}}^{-1}} \\\ \end{aligned}$
It is the minimum amount of energy required by the $\text{ OH }$ radical to undergo the reaction to form water and oxygen atoms.
Therefore, the activation energy for the backward reaction is $5\text{ kJ mo}{{\text{l}}^{-1}}$.

Hence, (C) is the correct option.

Note:
Note that, in the above reaction the reactant liberates energy to form low energy products, thus this is an exothermic reaction and therefore we have taken the negative value of enthalpy. However, there is a certain reaction in which the product acquires a larger energy than the reactant. This is an endothermic reaction and heat change in such a reaction is considered positive. In an endothermic reaction, the activation energy for the backward reaction would be equal to,
$\text{ E}{{\text{a}}_{\text{(Backward)}}}\text{ = E}{{\text{a}}_{\text{(forward)}}}\text{ + }\Delta {{\text{H}}_{\text{(endothermic)}}}$