Question

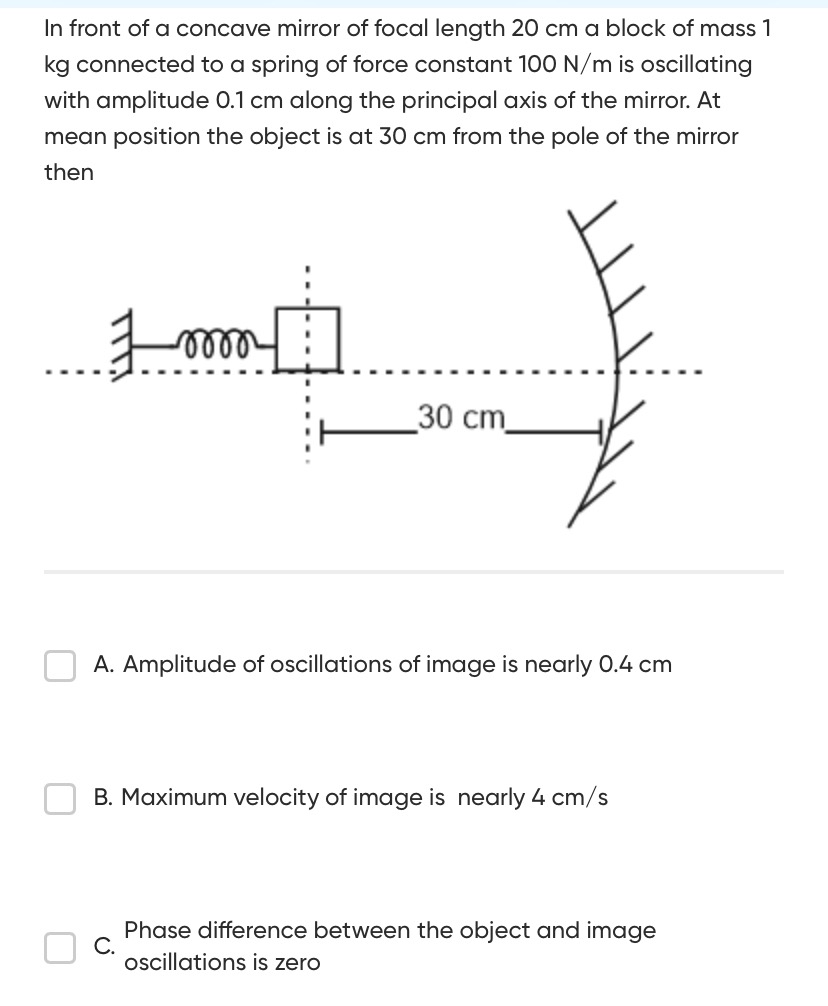
In front of a concave mirror of focal length 20 cm a block of mass 1 kg connected to a spring of force constant 100 N/m is oscillating with amplitude 0.1 cm along the principal axis of the mirror. At mean position the object is at 30 cm from the pole of the mirror then

• A. Amplitude of oscillations of image is nearly 0.4 cm
• B. Maximum velocity of image is nearly 4 cm/s
• C. Phase difference between the object and image oscillations is zero

Answer 1

Answer: (A), (B)

A, B

Answer 2

1. Determine Image Position and Magnification at Mean Position:

Given:

• Focal length of concave mirror, $f = -20$ cm (using sign convention, real focus is negative).
• Object distance at mean position, $u = -30$ cm.

Using the mirror formula: $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$ $\frac{1}{v} = \frac{1}{f} - \frac{1}{u} = \frac{1}{-20} - \frac{1}{-30} = -\frac{1}{20} + \frac{1}{30}$ $\frac{1}{v} = \frac{-3 + 2}{60} = \frac{-1}{60}$ $v = -60$ cm.

The image is real and formed at 60 cm from the pole on the same side as the object.

The transverse magnification $m$ at the mean position is: $m = -\frac{v}{u} = -\frac{-60}{-30} = -2$.

2. Determine Angular Frequency and Maximum Velocity of Object:

Given:

• Mass of block, $m_{block} = 1$ kg.
• Force constant of spring, $k = 100$ N/m.
• Amplitude of object oscillation, $A_o = 0.1$ cm $= 0.001$ m.

The angular frequency of oscillation $\omega$ is: $\omega = \sqrt{\frac{k}{m_{block}}} = \sqrt{\frac{100 \text{ N/m}}{1 \text{ kg}}} = \sqrt{100} = 10$ rad/s.

The maximum velocity of the object $V_{o,max}$ is: $V_{o,max} = A_o \omega = (0.1 \text{ cm}) \times (10 \text{ rad/s}) = 1 \text{ cm/s}$.

3. Analyze Image Oscillations:

A. Amplitude of oscillations of image ($A_i$):

For small longitudinal oscillations, the relationship between object displacement $\Delta u$ and image displacement $\Delta v$ is given by the longitudinal magnification $m_L = \frac{dv}{du}$.

Differentiating the mirror formula $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$ with respect to $u$: $-\frac{1}{v^2}\frac{dv}{du} - \frac{1}{u^2} = 0$ $\frac{dv}{du} = -\frac{v^2}{u^2}$.

So, $m_L = -\left(\frac{v}{u}\right)^2$.

Since $m = -\frac{v}{u}$, we have $m_L = -m^2$.

The amplitude of image oscillation $A_i$ is related to the object's amplitude $A_o$ by: $A_i = |m_L| A_o = |-m^2| A_o = m^2 A_o$.

Substituting the value of $m$: $A_i = (-2)^2 \times (0.1 \text{ cm}) = 4 \times 0.1 \text{ cm} = 0.4 \text{ cm}$.

Thus, option A is correct.

B. Maximum velocity of image ($V_{i,max}$):

The velocity of the image $V_i = \frac{d(\Delta v)}{dt}$ and the velocity of the object $V_o = \frac{d(\Delta u)}{dt}$.

From $\Delta v = m_L \Delta u = -m^2 \Delta u$, differentiating with respect to time gives: $V_i = -m^2 V_o$.

The maximum velocity of the image is: $V_{i,max} = |-m^2| V_{o,max} = m^2 V_{o,max}$. $V_{i,max} = 4 \times (1 \text{ cm/s}) = 4 \text{ cm/s}$.

Thus, option B is correct.

C. Phase difference between the object and image oscillations:

From the relation $\Delta v = -m^2 \Delta u$, since $m^2$ is always positive, $\Delta v$ and $\Delta u$ always have opposite signs. This means if the object moves in one direction from its mean position, the image moves in the opposite direction from its mean position.

For example, if the object moves towards the mirror ($\Delta u$ is negative), the image moves away from the mirror ($\Delta v$ is positive).

This indicates a phase difference of $\pi$ radians ($180^\circ$) between the oscillations of the object and its image.

Therefore, option C, which states the phase difference is zero, is incorrect.