Question

In Fresnel’s biprism experiment, when light of wavelength $6000A{}^\circ$ is used, ${{16}^{th}}$ bright fringe is obtained at point $P$. If light of wavelength $4800A{}^\circ$ is used, then the order of fringe obtained at point $P$ will be
A) ${{16}^{th}}$
B) ${{20}^{th}}$
C) ${{18}^{th}}$
D) ${{24}^{th}}$

Answer 1

Fresnel’s biprism experiment is a special case of Young’s double slit experiment. The fringe widths obtained through both the experiments have similar formulas. The order of fringe at a particular point due to a monochromatic light source can be determined by comparing its fringe width to the fringe width obtained using another monochromatic light source at the same point.

Complete answer:
Fresnel’s biprism experiment is a variation of Young’s double slit experiment. In Fresnel’s biprism experiment, two prisms which are connected through their bases are used. When monochromatic light of a particular wavelength is allowed to fall on this setup, an interference pattern involving bright and dark fringes is observed on a screen kept on the other side of the biprism. It is seen that the interference pattern is concentrated at the centre of the screen and appears to fall from two virtual sources of monochromatic light behind the prism. Thus, this experiment is similar to Young’s double slit experiment, which uses two light sources. The fringe width obtained using Fresnel’s biprism and that obtained using Young’s double slit experiment have the same formulas.

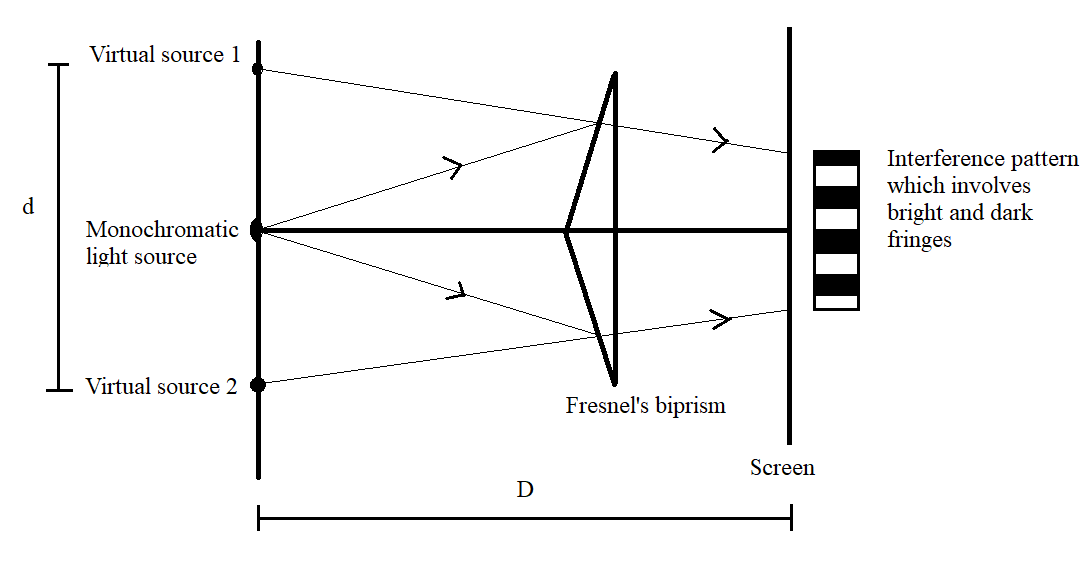
In Fresnel’s biprism experiment, the fringe width is given by
$\beta =\dfrac{\lambda D}{d}$
where
$\beta$ is the fringe width
$D$ is the distance between the virtual light sources and the screen
$d$ is the distance between the virtual light sources.
Let this be equation 1.
From the question, we are provided that a monochromatic light of wavelength $6000A{}^\circ$ is used in the first trial. Let this wavelength be represented as ${{\lambda }_{1}}$. Also, let the fringe width in the interference pattern due to this light source be ${{\beta }_{1}}$. This fringe width is calculated using equation 1 as shown below.
${{\beta }_{1}}=\dfrac{{{\lambda }_{1}}D}{d}=\dfrac{6000D}{d}$
Let this be equation 2.
It is also given that the ${{16}^{th}}$ bright fringe in the interference pattern is obtained at a point $P$. We know that the fringe width of a bright fringe of a particular order is given by
${{\beta }_{n}}=n\dfrac{\lambda D}{d}$
where
$n$ is the order of the fringe
${{\beta }_{n}}$ is the fringe width of a bright fringe of ${{n}^{th}}$ order
Therefore, the fringe width of ${{16}^{th}}$ bright fringe is given by
${{\beta }_{16}}=16\dfrac{\lambda D}{d}$
Let this be equation 3.
Substituting equation 2 in equation 3, we have
${{\beta }_{16}}=16\dfrac{\lambda D}{d}=\dfrac{16\times 6000D}{d}$
Let this be equation 4.
Now, let us move on to the second trial, where a monochromatic light source of wavelength $4800A{}^\circ$ is used to obtain fringes. Let this wavelength be represented as ${\lambda }'$ and let the fringe width be represented as ${\beta }'$. From equation 1, it is clear that ${\beta }'$ is given by
${\beta }'=\dfrac{{\lambda }'D}{d}=\dfrac{4800D}{d}$
Let this be equation 5.
Now, the fringe width of a fringe of a particular order $n$ obtained at point $P$ due to this source of light is given by
${{{\beta }'}_{n}}=n\dfrac{{\lambda }'D}{d}=\dfrac{n\times 4800D}{d}$
Let this be equation 6.
To determine the value of $n$, we divide equation 4 by equation 6 and equate it to one as follows.
$\dfrac{{{\beta }_{16}}}{{{{{\beta }'}}_{n}}}=1\Rightarrow \dfrac{\dfrac{16\times 6000D}{d}}{\dfrac{n\times 4800D}{d}}=1\Rightarrow \dfrac{16\times 6000}{n\times 4800}=1\Rightarrow n=\dfrac{16\times 6000}{4800}=20$
Therefore, the order of fringe at the point $P$ when a light of wavelength $4800A{}^\circ$ is used, is equal to $20$.

So, the correct answer is “Option B”.

Note:
In the last step, to obtain the value of $n$, we divide equation 4 by equation 6 and equate the expression to one. The reason behind this method of calculation is that the fringe width remains the same at a particular point in the interference pattern. Here, point $P$ is not moving and the fringe widths due to lights of wavelengths $6000A{}^\circ$ and $4800A{}^\circ$ are the same here. Only the orders of the fringes change.