Question
Question: In Figure, what is the potential difference \({V_d} - {V_c}\) between point d and c if \({E_1} = 0.4...
In Figure, what is the potential difference Vd−Vc between point d and c if E1=0.4V, E2=1.0V ,R1=R2=10Ω, and R3=5.0Ω, and the battery is ideal.
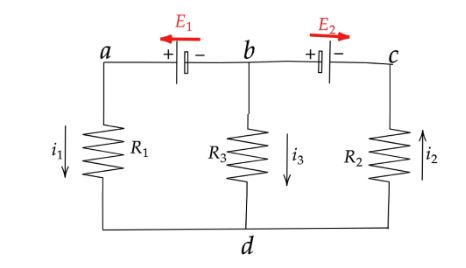
Solution
Here we have to find the potential difference between the two terminals d and c. First we will find the values of their difference current in diffract branches of the circuit using the given information. Then after taking two different paths one is branch d to b to c and the other one is d to c hence from that we will get two same potential difference values for both the way.
Complete step by step answer:
As per the given problem we have a figure where E1=4.0V, E2=1.0V ,R1=R2=10Ω, and R3=5.0Ω, and the battery is ideal.Now we need to calculate the value of potential difference Vd−Vc between point d and c.Now from the above given figure we can write,
i1=R1R2+R2R3+R1R3E1(R2+R3)−E2R3
We know,
E1=4.0V
⇒E2=1.0V
⇒R1=R2=10Ω
⇒R3=5.0Ω
Now putting the given values we will get,
i1=(10Ω)(10Ω)+(10Ω)(5Ω)+(10Ω)(5Ω)(4.0V)(10Ω+5Ω)−(1.0V)(5Ω)
On further solving and simplifying we will get,
i1=0.275A
Similarly from the figure we can write,
i2=R1R2+R2R3+R1R3E1R3−E2(R1+R2)
We know,
E1=4.0V
⇒E2=1.0V
⇒R1=R2=10Ω
⇒R3=5.0Ω
Now putting the given values we will get,
i2=(10Ω)(10Ω)+(10Ω)(5Ω)+(10Ω)(5Ω)(4.0V)(5Ω)−(1.0V)(10Ω+5Ω)
On further solving and simplifying we will get,
i2=0.025A
Now from the figure we can write,
i3=i2−i1=0.025A−0.275A=−0.250A
Now to find the potential differ,
We can two different oath two calculate the potential difference
Case I: From point d to b to c we will get,
Vd+i3R3+E2=Vc
We know,
i3=−0.250A
⇒R3=5.0Ω
⇒E2=1.0V
Now putting the known value we will get,
Vd+(−0.250A)(5Ω)+1.0V=Vc
On soling we will get,
Vd−0.250V=Vc
On rearranging we will get,
Vd−Vc=0.250V
Case II: From point d to c we will get,
Vd−i2R2=Vc
We know,
i2=0.025A
⇒R2=10Ω
Now putting the known value we will get,
Vd−(0.025A)(10Ω)=Vc
On soling we will get,
Vd−0.250V=Vc
On rearranging we will get,
∴Vd−Vc=0.250V
Hence,the potential difference Vd−Vc between point d and c is 0.250 V.
Note: Remember that potential difference is the difference in the amount of energy that a charge carrier has between two points in a circuit as in this equation the two points are d and c. Note that whatever the path the current has travelled, the potential difference between that point will always remain the same and it is measured in terms of voltage.
