Question
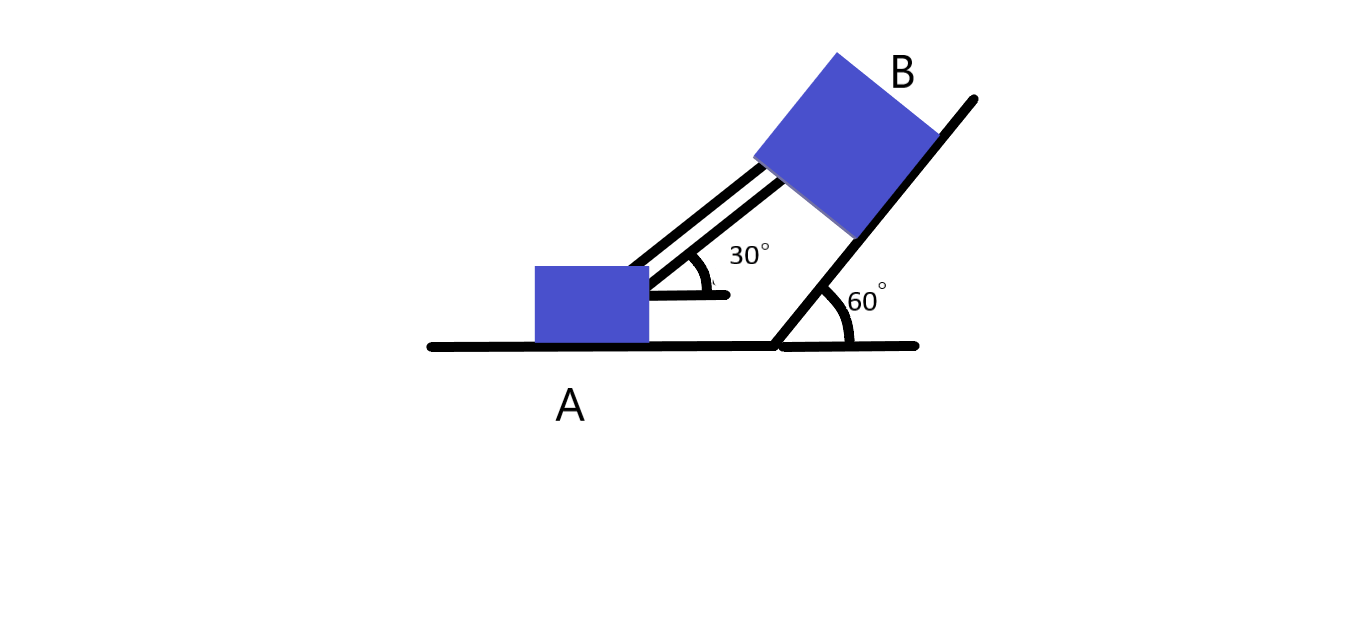
Question: In figure, two blocks are separated by a uniform strut attached to each block with frictionless pins...
In figure, two blocks are separated by a uniform strut attached to each block with frictionless pins, block A weighs 400N , block B weighs 300N and the strut AB weigh 200N . If μ=0.25 under B , determine the minimum coefficient of friction under A to prevent motion.
\left( A \right)0.4 \\\
\left( B \right)0.2 \\\
\left( C \right)0.8 \\\
\left( D \right)0.1 \\\
Solution
Hint : In order to solve this question, we are first going to draw the free body diagrams for the three structures, the strut, the block at point A and that at the point B . After that, we are going to write the equilibrium equations for the three and try to find out the forces acting on the elements, then the coefficient of friction is found.
Formula used: The free body diagram and its equilibrium conditions can be used to solve this question.
The frictional force that is acting on the two blocks is given by the formula.
FA=μANA
Complete Step By Step Answer:
Consider the free body diagram of the structure, for the strut and for the two blocks
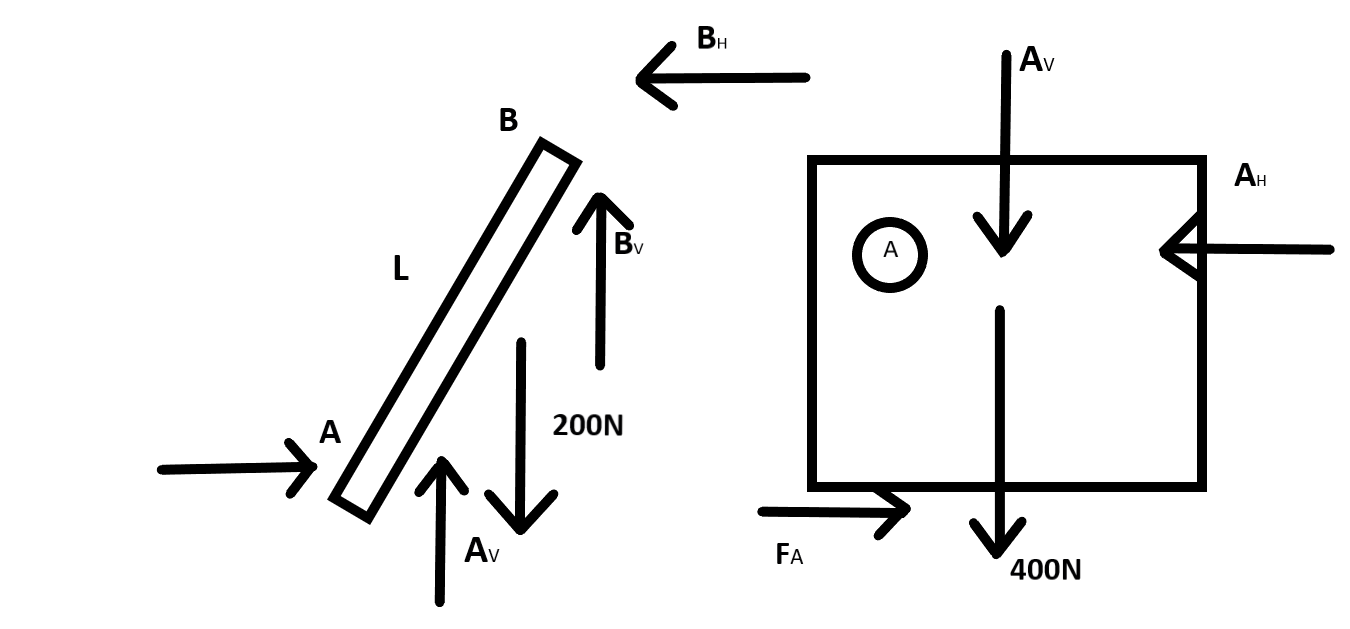
For free body diagram of the strut, applying the equilibrium equations
{A_V} + {B_V} = 200N - - - \left( i \right) \\\
{A_H} = {B_H} - - - - \left( {ii} \right) \\\
Where AH and AV are the horizontal components of the forces due to A
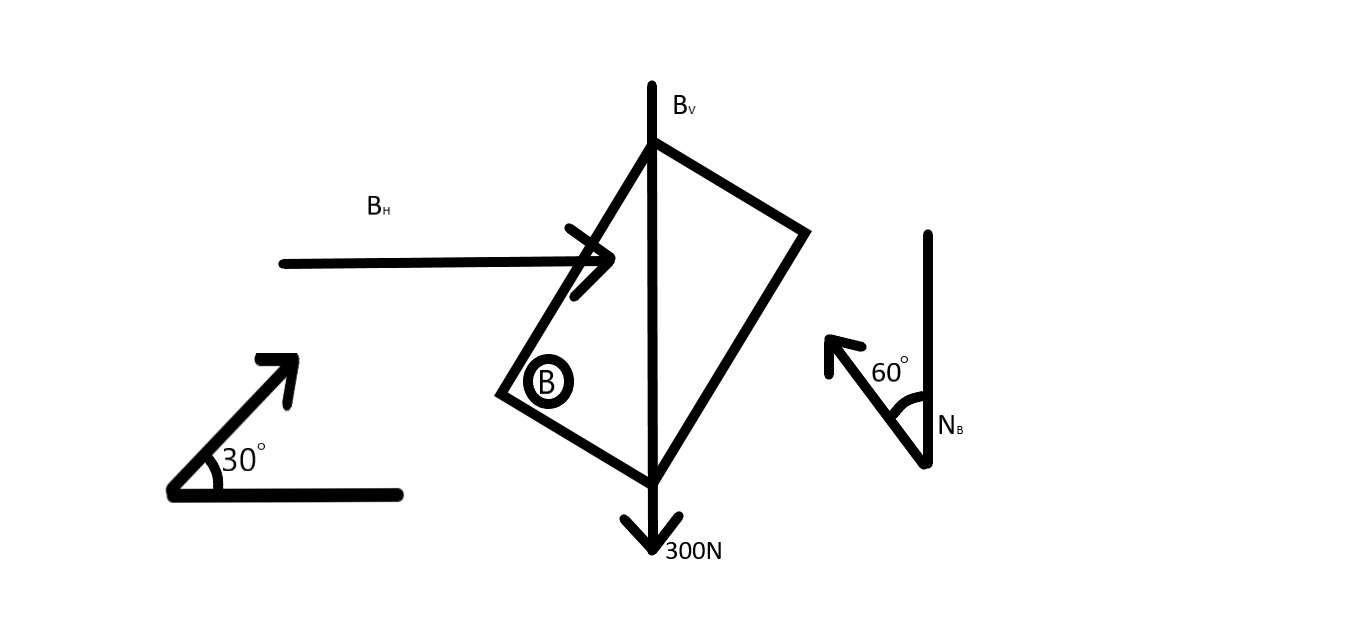
For the block B
{B_H} + {F_B}\cos {60^ \circ } - {N_B}\sin {60^ \circ } = 0 \\\
{N_B}cos{60^ \circ } - {B_V} - 300 + {F_V}sin{60^ \circ } = 0 \\\
Now as we know that
FB=0.25NB
Thus the above equations become
{B_H} - 0.74{N_B} = 0.....(iii) \\\
\- {B_V} + 0.71{N_B} = 300.....(iv) \\\
Now for the block A
{F_A} - {A_H} = 0.....(v) \\\
{N_{A}} - {A_V} = 400 \\\
As we know that
FA=μANA
Putting this in (v) , we get
∴μANA−AH=0.....(vi)
Thus, on solving these equations, we get
NA=650N
FA=260N
Now as we already know that
FA=μANA
Therefore, we get
μA=250260=0.4
Note :
It is important to note that you cannot just put the equations for the forces of friction, gravity and other directly to show the equilibrium conditions of the strut and the blocks, it is very important to have a free body diagram for the three to give us an insight of what the directions of the forces are and what effect they are having.
