Question

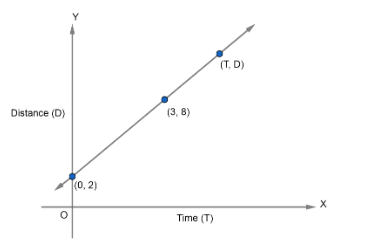
In figure, time and distance graph of a linear motion is given. Two positions of time and distance are recorded as, when T = 0, D = 2 and T = 3, D = 8. Using the concept of slope, find the law of motion, i.e., how distance depends upon time.

Answer 1

Hint: We will be using the concept of coordinate geometry to solve the problem. We will be using the fact that the equation of line passing through two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( y-{{y}_{1}} \right)=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$.

Complete step-by-step answer:

Now, we have been given the T vs D graph of a linear motion and two points which satisfy the line. So, we have,

Now, we know that the equation of a line passing through two points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ is
$\left( y-{{y}_{1}} \right)=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$.
So, we have to find the equation between time and distance that is the equation of a given line. So, we have,
$\begin{aligned} & \left( y-8 \right)=\left( \dfrac{8-2}{3-0} \right)\left( x-0 \right) \\\ & \left( y-8 \right)=\dfrac{5}{3}x \\\ & y=8+\dfrac{5}{3}x \\\ & y=\dfrac{5}{3}x+8 \\\ \end{aligned}$
Now, since on y – axis we have distance D and on x – axis we have time T. So, the equation of the given line is,
$D=8+\dfrac{5}{3}T$

Note: To solve these type of question it is important to note that we have used two point form of a straight line in which a line can be represented as,
$\left( y-{{y}_{1}} \right)=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right)$
Now, here $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ is slope of the line. So, we have utilised that concept also.