Question
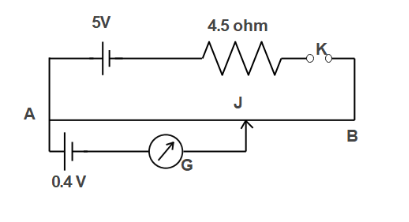
Question: In figure, the potentiometer wire AB has a resistance of \(5\) ohm and length \(10 m\). The balancin...
In figure, the potentiometer wire AB has a resistance of 5 ohm and length 10m. The balancing length AJ for the cell of e.m.f. of 0.4m is:
Solution
The potentiometer is based on the theory of potential gradient and null deflection. So, to work problems on the potentiometer, we should find a potential gradient and later for a null location. The galvanometer has a null point as the potential difference is equivalent to zero, and there is no current flow.
Complete step-by-step solution:
The potentiometer consists of L, along the resistive wire, and a battery of known EMF V, known as driver cell voltage. Consider a primary circuit arrangement by joining the two ends of L to the battery ends. One end of the primary circuit is joined to the cell whose EMF E is to be estimated, and the other end is joined to galvanometer G. This circuit is supposed to be a secondary circuit.
The practical principle depends on the potential to cross any portion of the wire, which is directly proportional to the wire length with a uniform cross-sectional area, and current movement is constant.
E=KL ……(i)
L: length of potentiometer wire
E: EMF
K: potential gradient
Put E=iR (ohm’s law) …...(ii)
Equate both equations, we get
K=LiR ……(iii)
R is the resistance of length of wire L.
i is the current.
R=5ohm
i=4.5+55=0.526A
L=10m
Put all values in (iii), we get
K=100.526×5=0.236
Now we have to find the balancing length for 0.4V:
E=KL
⟹0.4=0.263×L
L=0.2630.4=1.52m
The balancing length AJ for the cell of e.m.f. of 0.4V is 1.52m.
Note: The potentiometer is a simplistic device used to estimate electrical potentials. One form is a uniform high-resistance wire joined to insulating support. In use, a flexible regulated voltage source E, of higher magnitude than the potential to be estimated, is combined across the wire to transfer a steady current into it.
