Question
Question: In figure, sides QP and QR of \[\Delta PQR\] are produced to points T and S respectively. If \[\angl...
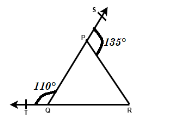
In figure, sides QP and QR of ΔPQR are produced to points T and S respectively. If ∠TQP=110∘ and ∠SPR=135∘, then find the value of ∠PRQ.
Solution
One sufficient information for solving this question is that the sum of all angles of a triangle is 180∘. So, by using this concept we can solve for the value of ∠PRQ. We are going to apply the concept of linear pair (when a line intersects another line at an angle, the two angles formed make a linear pair, and the sum of the two angles of a linear pair is 180∘).
So, first we are going to apply the concept of linear pair to the angle ∠SPR and then to the angle ∠TQP and find their corresponding linear pair and then use the angle sum property of triangle to solve for the value of ∠PRQ.
Formula Used:
We are going to use the concept of angle sum property of a triangle – the sum of all angles of a triangle is 180∘, which hence, is:
∠PQR+∠QPR+∠PRQ=180∘
Complete step by step solution:
In this question, we need to solve for the value of ∠PRQ which is in the ΔPQR.
First, we calculate the other angles of the triangle. We have been given the value of ∠SPR and ∠TQP and we need to calculate the angles adjacent to them.
And we can easily do that by applying the concept of linear pair.
∠SPR=135∘ and ∠TQP=110∘
So, first we solve for ∠QPR:
∠SPR+∠QPR=180∘
Hence, ∠QPR=180∘−135∘=45∘
Now, we solve for ∠PQR
∠TQP+∠PQR=180∘
Hence, ∠PQR=180∘−110∘=70∘
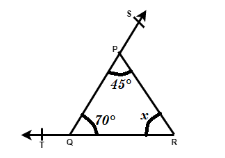
So, now we have two out of three angles of a triangle and we need to solve for the third unknown angle. And we can easily do that by applying the concept of the angle sum property, so we have:
∠PQR+∠QPR+∠PRQ=180∘
70∘+45∘+x=180∘
115∘+x=180∘
x=180−115=65∘
Hence, ∠PRQ=65∘
Note: So, we saw that in solving questions like these, we need to see what information we have got with us. Like here, we used the concept of angle sum property of triangle, because the figure clearly gave a triangle. Then we applied the concept of linear pair, because the angles in the triangle which we needed to find for calculating the ∠PRQ and the angles whose measure is given lie on a straight line, hence forming a linear pair. The biggest giveaway is always what shape the figure is; we figure that out, we know in which direction we need to go.
