Solveeit Logo
Login

Question

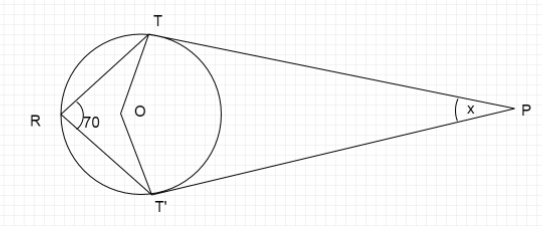
Question: In figure \[PT\]and \[PT'\]are tangents to the circle with center \[O\]. If \[\angle TRT' = {70^ \ci...

In figure PTPTand PT′PT'are tangents to the circle with center OO. If ∠TRT′=70∘\angle TRT' = {70^ \circ }then xxequals
A. 30∘{30^ \circ }
B. 35∘{35^ \circ }
C. 40∘{40^ \circ }
D. 50∘{50^ \circ }

Explanation

Solution

Here we use the property which states that tangents meet the radius of the circle at right angles. We find all the angles of the quadrilateral TOT′PTOT'P and then using the property that the sum of all angles of a quadrilateral is 360∘{360^ \circ } we find the value of xx.
Also, angle subtended by the same arc at the center of the circle is twice the angle subtended by that arc at any other point on the circumference.

Complete step-by-step answer:
First we calculate the value of ∠TOT′\angle TOT'
Since, ∠TRT′=70∘\angle TRT' = {70^ \circ }
Therefore, using the theorem which states that angle subtended by an arc of a circle at its center is twice of the angle it subtends anywhere on the circumference of the circle.
Here the arc which is subtending the angles is arc
The angle subtended by the arc at the circumference is TRT′TRT'and the angle subtended by the arc at the center of the circle is ∠TOT′\angle TOT'
From the theorem, ∠TOT′=2×TRT′\angle TOT' = 2 \times TRT'
Substituting the value of ∠TRT′=70∘\angle TRT' = {70^ \circ }
∠TOT′=2×70∘=140∘\angle TOT' = 2 \times {70^ \circ } = {140^ \circ }
Now, since we know that tangent at a point meet the radius of circle at a right angle
Therefore, two tangents PT,PT′PT,PT' make angle 90∘{90^ \circ }at points T,T′T,T'.
Therefore, ∠OTP=∠OT′P=90∘\angle OTP = \angle OT'P = {90^ \circ }
Now we look at the quadrilateral TOT′PTOT'P
Sum of all angles is 360∘{360^ \circ }
∠OTP+∠TPT′+∠OT′P+∠T′OT=360∘\angle OTP + \angle TPT' + \angle OT'P + \angle T'OT = {360^ \circ }
Now we substitute the values of angles in the equation

90∘+x+90∘+140=360∘ x+320∘=360∘  {90^ \circ } + x + {90^ \circ } + 140 = {360^ \circ } \\\ x + {320^ \circ } = {360^ \circ } \\\

Taking the constant terms on one side of the equation
x=360∘−320∘=40∘x = {360^ \circ } - {320^ \circ } = {40^ \circ }
Thus, the value of x=40∘x = {40^ \circ }
So, option C is correct.

Note: Alternate method:
Join TT′TT'which forms a chord for the circle.

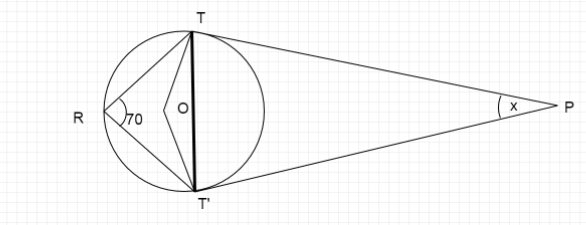
We calculate the value of ∠TOT′\angle TOT'
Since, ∠TRT′=70∘\angle TRT' = {70^ \circ }
Therefore, using the theorem which states that angle subtended by an arc of a circle at its center is twice of the angle it subtends anywhere on the circumference of the circle.
Here the arc which is subtending the angles is arc
The angle subtended by the arc at the circumference is TRT′TRT'and the angle subtended by the arc at the center of the circle is ∠TOT′\angle TOT'
From the theorem, ∠TOT′=2×TRT′\angle TOT' = 2 \times TRT'
Substituting the value of ∠TRT′=70∘\angle TRT' = {70^ \circ }
∠TOT′=2×70∘=140∘\angle TOT' = 2 \times {70^ \circ } = {140^ \circ }
Therefore in △TOT′\vartriangle TOT' sum of all angles is 180∘{180^ \circ }
Therefore, ∠TOT′+∠OTT′+∠OT′T=180∘\angle TOT' + \angle OTT' + \angle OT'T = {180^ \circ }
Both sides TO,T′OTO,T'O of the △TOT′\vartriangle TOT' are same because they are equal to radius of the circle.
Therefore, △TOT′\vartriangle TOT' is an isosceles triangle.
So, from the property of isosceles triangle having angles opposite to equal sides are equal.
∠OTT′=∠OT′T\angle OTT' = \angle OT'T
So the sum ∠TOT′+∠OTT′+∠OT′T=180∘\angle TOT' + \angle OTT' + \angle OT'T = {180^ \circ } becomes

140∘+∠OTT′+∠OTT′=180∘ 140∘+2∠OTT′=180∘  {140^ \circ } + \angle OTT' + \angle OTT' = {180^ \circ } \\\ {140^ \circ } + 2\angle OTT' = {180^ \circ } \\\

Take all constants to one side of the equation

2∠OTT′=180∘−140∘ 2∠OTT′=40∘  2\angle OTT' = {180^ \circ } - {140^ \circ } \\\ 2\angle OTT' = {40^ \circ } \\\

Divide both sides of the equation by 22

2∠OTT′2=40∘2 ∠OTT′=20∘  \dfrac{{2\angle OTT'}}{2} = \dfrac{{{{40}^ \circ }}}{2} \\\ \angle OTT' = {20^ \circ } \\\

∠OTT′=∠OT′T=20∘\angle OTT' = \angle OT'T = {20^ \circ }
Now, since we know that tangent at a point meet the radius of circle at a right angle
Therefore, two tangents PT,PT′PT,PT' make angle 90∘{90^ \circ }at points T,T′T,T'.
Therefore, ∠OTP=∠OT′P=90∘\angle OTP = \angle OT'P = {90^ \circ }

∠OTP=90∘ ∠OTT′+∠T′TP=90∘ 20∘+∠T′TP=90∘ ∠T′TP=90∘−20∘=70∘  \angle OTP = {90^ \circ } \\\ \angle OTT' + \angle T'TP = {90^ \circ } \\\ {20^ \circ } + \angle T'TP = {90^ \circ } \\\ \angle T'TP = {90^ \circ } - {20^ \circ } = {70^ \circ } \\\

Similarly,

∠OT′P=90∘ ∠OT′T+∠TT′P=90∘ 20∘+∠TT′P=90∘ ∠TT′P=90∘−20∘=70∘  \angle OT'P = {90^ \circ } \\\ \angle OT'T + \angle TT'P = {90^ \circ } \\\ {20^ \circ } + \angle TT'P = {90^ \circ } \\\ \angle TT'P = {90^ \circ } - {20^ \circ } = {70^ \circ } \\\

Now using the property of sum of all three angles of a triangle is 180∘{180^ \circ }
∠TT′P+∠T′TP+∠TPT′=180∘\angle TT'P + \angle T'TP + \angle TPT' = {180^ \circ }
Substituting the values of angles

70∘+70∘+x=180∘ 140∘+x=180∘  {70^ \circ } + {70^ \circ } + x = {180^ \circ } \\\ {140^ \circ } + x = {180^ \circ } \\\

Shift all constants to one side of the equation.
x=180∘−140∘=40∘x = {180^ \circ } - {140^ \circ } = {40^ \circ }
So, option C is correct.