Question

In figure, if ABCDEF is a regular hexagon, calculate appropriate length of AE if AB$= 4$

Answer 1

We know that all the interior angles of a regular hexagon are equal and of $120^\circ$ and triangles between the diagonal AE are congruent to each other, use the properties of triangle to find GE.

Complete step-by-step answer:
Given hexagon is a regular type. So each interior angle will be equal.
So, angles are$\dfrac{{720}}{6}$ (total sum of interior angles of a regular hexagon is $720^\circ$) .
Now, join A and E, and then draw a perpendicular from F to the line AE which will be FG
On AE we will see that perpendicular bisects AE in AG and GE as triangles FGA and triangle FGE are congruent to each other.

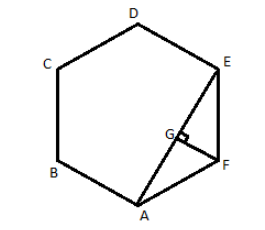
So, in triangle FGE, we will apply the trigonometric functions of the right angled triangle as triangle FGE is a right angled triangle.
$\sin 60^\circ = \dfrac{{GE}}{{EF}}{\text{ }} \to \left( 1 \right)$
Let GE be equal to$x$.
And we know that $GE = AG$
Then, AG will also be equal to $x$
Now, we will find AE as $AE = AG + GE$ .
$AE = x + x \\\ = 2x \\\$
And we know that all sides of hexagon are equal to each other so we have given that $AB = 4$
Which means, $EF = 4$
So, by putting these values of AB and GE in equation (1)
$\sin 60^\circ = \dfrac{x}{4} \\\ 0.866 = \dfrac{x}{4} \\\ 0.866 \times 4 = x \\\ 3.464 = x \\\$
Now, we have found that AE is equal to $2x$ .so, we will put the value of $x$ in $2x$ to find the value of AE.
$AE = 2x \\\ AE = 2\left( {3.464} \right) \\\ AE = 6.93 \\\$
So the value of AE will be $6.93$

Note: We have to do a construction in the hexagon by joining the points A and E to form a line and draw a perpendicular to the line AE from the point F which bisect the line AE.