Question

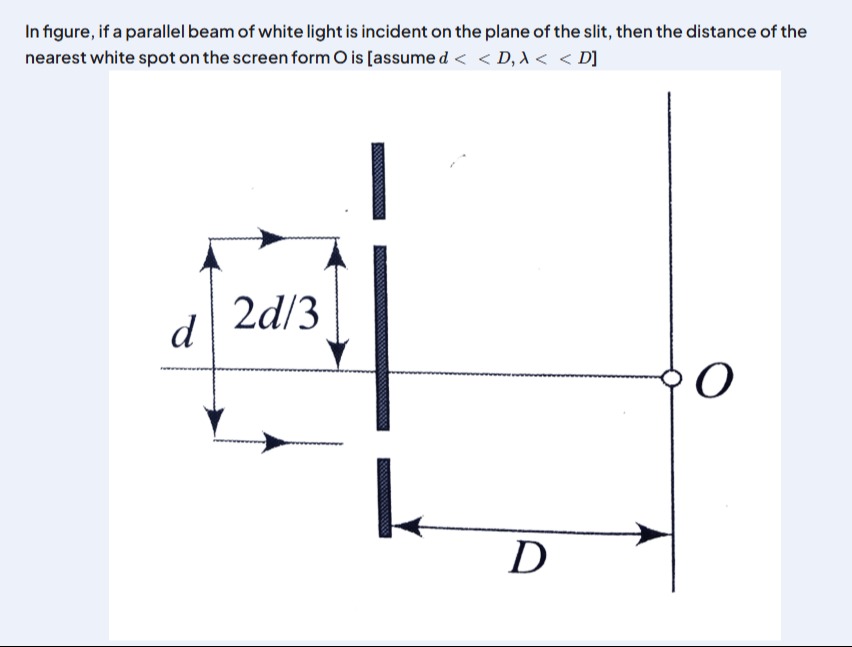
In figure, if a parallel beam of white light is incident on the plane of the slit, then the distance of the nearest white spot on the screen form O is [assume $d << D, \lambda << D$]

• A. $\frac{3\lambda D}{2d}$
• B. $\frac{2\lambda D}{d}$
• C. $\frac{\lambda D}{d}$
• D. $\frac{3\lambda D}{d}$

Answer 1

$\frac{3\lambda D}{2d}$

Answer 2

In single-slit diffraction of white light, the central maximum is white. The secondary maxima are spectrally dispersed. The question asks for the "nearest white spot" other than the central one. This implies we are looking for a position where the spectral dispersion results in a white appearance.

The condition for a secondary maximum in single-slit diffraction is given by $a \sin \theta = (2n+1) \frac{\lambda}{2}$, where $a$ is the slit width, $\theta$ is the angle of diffraction, $\lambda$ is the wavelength, and $n$ is an integer ($n=1, 2, 3, \dots$ for secondary maxima). For small angles, $\sin \theta \approx \tan \theta = \frac{y}{D}$, where $y$ is the distance from the center of the screen and $D$ is the distance from the slit to the screen. Thus, the position of the $n$-th secondary maximum is $y = \frac{(2n+1)\lambda D}{2a}$.

For white light, the visible spectrum ranges from approximately $\lambda_{violet} \approx 400$ nm to $\lambda_{red} \approx 700$ nm. The first secondary maximum ($n=1$) occurs at $y = \frac{3\lambda D}{2a}$. For white light, this position will be a spectrum, with red light diffracted at a larger angle (further from the center) than violet light. So, the first secondary maximum is not a pure white spot.

However, in some specific cases of diffraction or interference with white light, a white fringe can be observed at positions other than the central maximum. This typically happens when the path difference or phase difference condition for constructive interference is met for a range of wavelengths, or when the dispersion leads to a cancellation of colors.

Let's assume that the diagram indicates that the slit width is $a=d$. The question asks for the "nearest white spot" on the screen from O. The central maximum at $y=0$ is white. The first secondary maxima occur at $y = \frac{3\lambda D}{2a}$ for different wavelengths. For white light, this will be a spectrum.

A common interpretation in such problems is that the question refers to the first secondary maximum where the dispersion is such that it appears predominantly white. This can happen if the slit width is very large compared to the wavelength, or under specific conditions not detailed here.

Given the options, and the typical context of such problems, it is most likely that the question is simplified and is asking for the position of the first secondary maximum, assuming the slit width $a=d$. In this case, for $n=1$, the position is $y = \frac{3\lambda D}{2d}$.

The phrase "nearest white spot" usually refers to the first secondary maximum that appears white. In single-slit diffraction of white light, the central maximum is white. The first-order maxima are typically colored, with red on the outside and violet on the inside. However, sometimes, under specific conditions or approximations, the question might refer to the first secondary maximum as a "white spot" if the dispersion is not very pronounced or if it's a simplified model.

Assuming the slit width is $a=d$, the condition for the $n$-th secondary maximum is $a \sin \theta = (2n+1)\frac{\lambda}{2}$. For small angles, $y \approx D \tan \theta \approx \frac{a \sin \theta}{D}$. So, $y_n = \frac{(2n+1)\lambda D}{2a}$. For the first secondary maximum ($n=1$), $y_1 = \frac{3\lambda D}{2a}$. If we assume $a=d$, then $y_1 = \frac{3\lambda D}{2d}$.

This corresponds to the first option. While strictly speaking, the first secondary maximum is a spectrum, in simplified problems, it might be referred to as a "white spot" if it's the first non-central bright fringe.