Question
Question: In figure, find the value of the resistor to be connected between C and D, so that the resistance of...
In figure, find the value of the resistor to be connected between C and D, so that the resistance of the entire circuit between A and B does not change with the number of elementary sets.
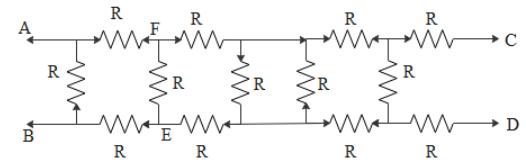
(A)R(B)R(3−1)(C)3R(D)R(3+1)
Solution
Consider the new resistance across CD as ‘x’. Then the equivalent resistance across CD will be the same as the resistance across AB and EF. When we take the resistance across CD as ‘x’, then resistance across AB and EF will also be ‘x’. Then draw the equivalent circuit and then find the resistance across AB. We have already considered that resistance across AB is x. Thus equate the both terms and using quadratic equation find the value of ‘x’ and that will be resistance across CD.
Complete answer:
Consider the new resistance across the CD as ‘x’. Then the equivalent resistance across CD will be the same as the resistance across AB and EF. When we take the resistance across CD as ‘x’, then resistance across AB and EF will also be ‘x’.
Thus let resistance across AB and EF be ‘x’. For this consider a part of the circuit as shown below.
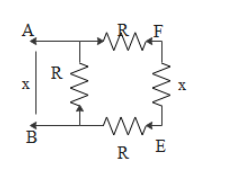
Then the equivalent circuit can be drawn as,
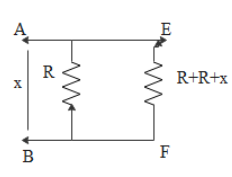
That is, here the three resistors R, x and R are connected in series.
Hence there equivalent resistance is,
Req=R+x+R⇒Req=2R+x
These two resistors are connected in parallel. Hence, resistance across AB is,
RAB1=R1+2R+x1
⇒RAB1=R(2R+x)2R+x+R⇒RAB=3R+xR(2R+x)
⇒RAB=x
Thus,
3R+xR(2R+x)=x
R(2R+x)=3Rx+x2
2R2+Rx=3Rx+x2
⇒x2+2Rx−2R2=0
Apply quadratic equations.
x=2a−b±b2−4ac
⇒x=2−2R±(2R)2−4×1×(−2R2)
Then,
x=2−2R±4R2+8R2
⇒x=2−2R±12R2
