Question
Question: In figure, final value of current in \(10\Omega \) resistor, when plug of key \(k\) is inserted. !...
In figure, final value of current in 10Ω resistor, when plug of key k is inserted.
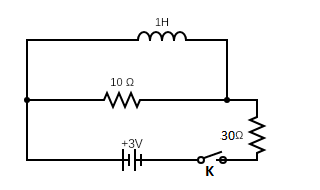
A) 103A
B) 203A
C) 113A
D) zero
Solution
When a current passes through a coil it produces a magnetic field around it. Flux due to this field is linked with the coil itself. If the current through the coil changes, the flux linked with it also changes. Hence an emf is induced in the coil.
Complete step by step answer:
Just after closing the key the inductor will be treated as an open circuit. so, the circuit would be like this.
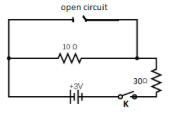
But here we need to calculate the final value of the current in the 10Ω resistor, for this key is closed for a long time. After a long time of closing the switch, the inductor is treated as a short circuit. So, the circuit would be like as shown in the figure.

Because of this short circuit, the entire current will be passing through that shorted path, there is no current through the 10Ω resistor.
∴ The Final value of current in the 10Ω resistor is zero.
Hence option D is correct
Additional information:
The phenomenon in which electric current is induced by varying magnetic fields is called electromagnetic induction.
Self-inductance is the property of a coil by virtue of which it opposes the growth or decay of the current flowing through it.
Note: Self-inductance is the electromagnetic analogue of mass in mechanics. Mass is a measure of inertia which is responsible for slowing down the change in mechanical motion of a body. Similarly, self-inductance slows down the change in the current in an electrical circuit. Therefore, self-inductance can be called as inertia of electricity. The self-induced emf always opposes the change in the current in a circuit and therefore, it is also known as a ‘back emf’. Work is needed to be done against this back emf in establishing current in the circuit.
