Question

In figure an arrangement of three identical capcitors is shown alongwith a switch S and a battery B. If the switch S is closed, then the ratio of the energy of the capacitors system in the final steady state to the initial state is :-

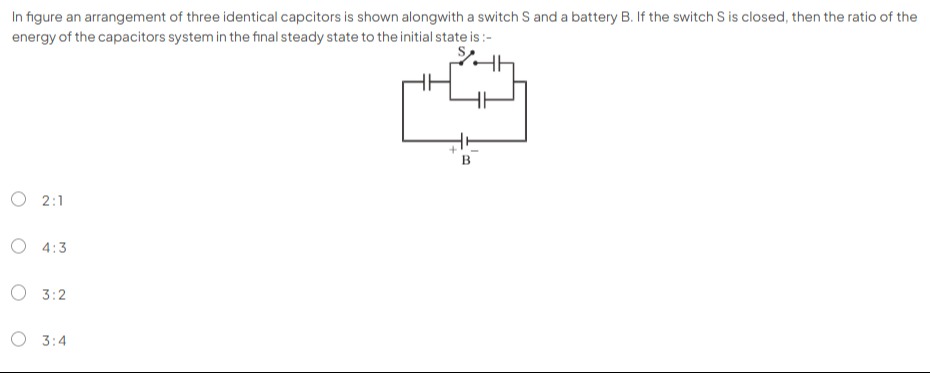
• A. 2:1
• B. 4:3
• C. 3:2
• D. 3:4

Answer 1

Answer: (B)

4:3

Answer 2

To solve this problem, we need to calculate the total energy stored in the capacitor system in two different states:

1. Initial state: When the switch S is open.
2. Final steady state: When the switch S is closed.

Let the capacitance of each identical capacitor be $C$, and the voltage of the battery be $V$. The energy stored in a capacitor system is given by the formula $U = \frac{1}{2} C_{eq} V^2$, where $C_{eq}$ is the equivalent capacitance of the system.

1. Initial State (Switch S is open)

When the switch S is open, the capacitor connected in the branch with the switch (let's call it $C_2$) is disconnected from the circuit. The circuit effectively consists of the other two capacitors ($C_1$ and $C_3$) connected in series across the battery.

Since the path with $C_2$ is open, only $C_1$ and $C_3$ are active in the circuit. They are connected in series. The equivalent capacitance for two capacitors in series is given by: $C_{eq, initial} = \frac{C_1 \times C_3}{C_1 + C_3} = \frac{C \times C}{C + C} = \frac{C^2}{2C} = \frac{C}{2}$

The energy stored in the initial state is: $U_{initial} = \frac{1}{2} C_{eq, initial} V^2 = \frac{1}{2} \left(\frac{C}{2}\right) V^2 = \frac{1}{4} C V^2$

2. Final Steady State (Switch S is closed)

When the switch S is closed, all three capacitors are part of the circuit.

This configuration means that $C_2$ and $C_3$ are connected in parallel, and this parallel combination is then connected in series with $C_1$.

First, calculate the equivalent capacitance of $C_2$ and $C_3$ in parallel: $C_{parallel} = C_2 + C_3 = C + C = 2C$

Now, this $C_{parallel}$ is in series with $C_1$. The total equivalent capacitance of the system in the final state is: $C_{eq, final} = \frac{C_1 \times C_{parallel}}{C_1 + C_{parallel}} = \frac{C \times (2C)}{C + 2C} = \frac{2C^2}{3C} = \frac{2C}{3}$

The energy stored in the final steady state is: $U_{final} = \frac{1}{2} C_{eq, final} V^2 = \frac{1}{2} \left(\frac{2C}{3}\right) V^2 = \frac{1}{3} C V^2$

3. Ratio of Energies

Finally, we need to find the ratio of the energy in the final steady state to the initial state ($U_{final} : U_{initial}$). Ratio = $\frac{U_{final}}{U_{initial}} = \frac{\frac{1}{3} C V^2}{\frac{1}{4} C V^2}$

Cancel out the common terms ($C V^2$): Ratio = $\frac{1/3}{1/4} = \frac{1}{3} \times \frac{4}{1} = \frac{4}{3}$

So, the ratio of the energy of the capacitors system in the final steady state to the initial state is 4:3.