Question

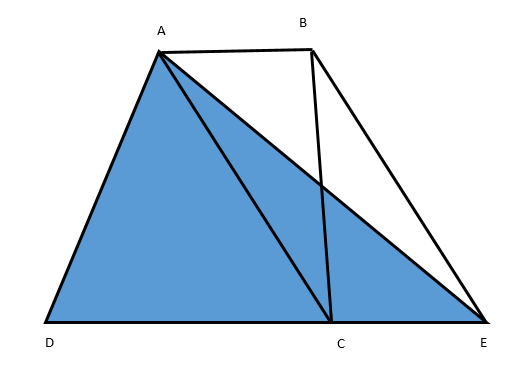
In figure, ABCD is a quadrilateral and BE || AC and also BE meets DC produced at E. Show that the area of $\vartriangle ADE$ is equal to the area of quadrilateral ABCD.

Answer 1

We will use some theorems to first prove that ar. (ABC) = ar. (ACE) and then just add up the area ar. (ADC) to both sides in order to get the required equality between the areas.

Step-By-Step answer:
Since, we can observe that $\vartriangle ABC$ and $\vartriangle ACE$ lie on the same base BC and are between same parallels that is BE || AC (given).
So, by using the theorem, which says that: “Triangles on the same base and between the same parallels have equal area”, we will get that:-
$\Rightarrow ar.(\vartriangle ABC) = ar.(\vartriangle ACE)$ …………….(1)
Now, we will add the area of the $\vartriangle ADC$ to both the sides of the equation (1) and we will then obtain the following expression:-
$\Rightarrow ar.(\vartriangle ABC) + ar.(\vartriangle ADC) = ar.(\vartriangle ACE) + ar.(\vartriangle ADC)$
Now, clearly observing these areas in the picture, we can combine them to get the following expression:-
$\Rightarrow ar.(\square ABCD) = ar.(\vartriangle ADE)$
Hence, we have proved the required equality.

$\therefore$ the area of $\vartriangle ADE$ is equal to the area of quadrilateral ABCD.

Note: The students must commit to memory the following theorem:-
Triangles on the same base and between the same parallels have equal area.
The students must note that committing the theorem to their memory does not mean they need to cram it, they must know the logic behind it. Let us discuss that briefly:-
We know that the area of the triangle is given by the half of the product of the base and height.
$\Rightarrow$ Area of a triangle = $\dfrac{1}{2} \times b \times h$, where b is the base of triangle and h is the height of triangle.
When we have two triangles on the same base, the value of b becomes the same for both of those triangles and then the height is obviously the length between both of the parallels. So, when both the triangles are in between the same parallels, the height will also remain the same for both and thus the value of area will be the same for both of the triangles.