Question
Question: In fig. The angle of inclination of the inclined plane is 30°. Find the horizontal velocity \({V}_{0...
In fig. The angle of inclination of the inclined plane is 30°. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
A.V=52gH
B.V=72gH
C.V=5gH
D.V=7gH
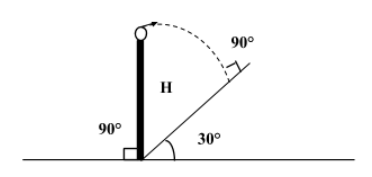
Solution
To solve this problem, first find the velocity of the particle along the Y axis using the Kinematic equation of motion showing relation between velocity and time. Substitute the values and find the value of time t. Then, use the kinematic equation of motion which gives the relation between displacement and time. Substitute the values in the kinematic equation and find the velocity. This will be the horizontal velocity of the particle that hits the inclined plane perpendicularly.
Complete answer:
Consider, X-axis is perpendicular to the plane and the Y-axis is parallel to the plane. So, when the particle hits the plane perpendicularly, its velocity becomes 0 along the X-axis.
Velocity of the particle along the Y-axis at time t will be,
v=u+at
Substituting the values in above equation we get,
0=V0cos30°+(−gsin30°)t
⇒gsin30°t=V0cos30°
⇒g×21×t=V023
⇒t=g3V0 …(1)
Displacement along the direction perpendicular to the plane is given by,
s=ut+21at2
Substituting the values in above equation we get,
Hcos30°=V0sin30°×g3V0+21gcos30°g3V02
⇒23H=2V0×g3V0+21g×23×g23V0
⇒23H=2g3V0+4g33V02
⇒2H=2gV02+4g3V02
⇒2H=4g2V02+4g3V02
⇒H=2g5V02
⇒V02=52gH
⇒V0=52gH
Hence, the horizontal velocity of the particle when it hits the inclined plane perpendicularly is 52gH.
Note:
To solve these types of problems, students should know all the equations of motions. They should also know the proper application of these equations. To choose the correct equation for the specified problem, check which parameters are given and which you are asked to find. If you want to find the displacement at a given time then use the equation, s=ut+21at2
If you have to find the displacement at given velocity, then use the relation, v2=u2+2as.
If you have to find the velocity at a given time then use the relation, v=u+at.
