Question
Question: In Fig. shown, both blocks are released from rest. Length of \( 4\;kg \) the block is \( 2\;m \) and...
In Fig. shown, both blocks are released from rest. Length of 4kg the block is 2m and of 1kg is 4m . Find the time they took to cross each other? Assume pulley to be light and string to be light and inelastic.
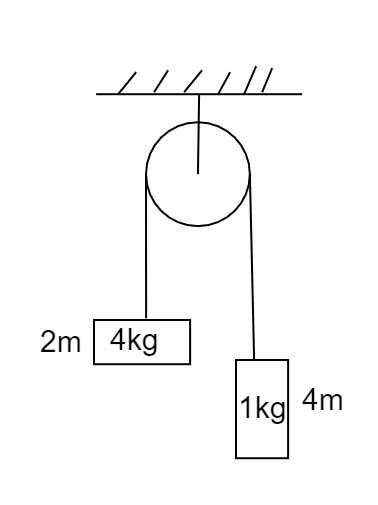
Solution
Here to find the time required by both blocks to cross each other, we will first evaluate the acceleration of the combined system. After that, we will use the equation of motions which relates the distance, time, and acceleration and by substitution, we will find the time required.
Formula used
Equation of motion
S=ut+21at2
where s is the distance, u is initial velocity, a is acceleration, and t is time.
Complete Step-by-step solution
We will first try to understand the system consist of a pulley and two blocks that are released from rest, as we can see from the figure that the block A is being heavier than the block B , hence the gravitational acceleration g on the block A would be 4g and on the block, B it would only g .
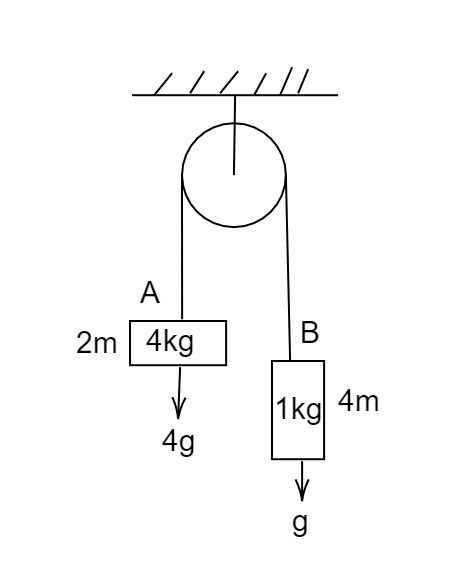
Now for both blocks, the friction between the blocks can be given as
For block A
⇒4g−T=4a ………. (1)
For block B
⇒T−g=a ………. (2)
Solving the equation (1) and (2) we the acceleration is given as
⇒a=4+14g−1g
⇒a=53g
Substituting the value of g=10m/s2 , hence it results in
⇒a=53×10m/s2
∴a=6m/s2
Now the relative acceleration of block A with respect to block B can be evaluated as
⇒a=2×6m/s2
⇒a=12m/s2
Now we will use the equation of motion which relates the distance, time, and acceleration given as
⇒S=ut+21at2
where s is the distance, u is initial velocity, a is acceleration, and t is time.
Now from the figure, it can be seen that the total distance covered by the blocks to cross each other is given as S=2m+4m=6m , and both blocks are released from rest hence the initial velocity can be given as u=0m/s .
Therefore substituting the values in the equation of motion results in
⇒6m=21×(12m/s2)×t2
⇒t=12m/s22×6m
∴t=1sec
Hence the time taken by both the blocks to cross each other when they are released from rest is t=1sec .
Note
Here in this question we have used the method of friction between the blocks method to find the acceleration. We have used gravitational acceleration which is g=9.8m/s2 but we have used g=10m/s2 it for our convenience as it is not provided in the question.
