Question
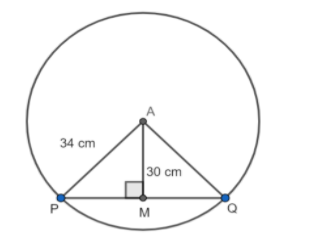
Question: In fig. point A is a center of a circle AP = 34 cm, A is the center of a circle, AM = 30 cm. If \[AM...
In fig. point A is a center of a circle AP = 34 cm, A is the center of a circle, AM = 30 cm. If AM⊥PQ , find the length of the chord PQ.
Solution
In the ΔAMP , we have AM = Perpendicular = 30 cm, AP = Hypotenuse = 34 cm, PM = Base, and ∠AMP=90∘ . Since the line segment, AM is perpendicular to the chord PQ so, we can apply the Pythagoras theorem in ΔAMP . We know the Pythagoras theorem, (Hypotenuse)2=(Perpendicular)2+(Base)2 . Now, apply the Pythagoras theorem in the ΔAMP and get the length of PM. We know the property that the perpendicular line drawn from the center to a chord of a circle bisects the chord. Here, AM is perpendicular to the chord PQ. So, the line AM bisects the chord PQ. M is the midpoint of the chord PQ. Therefore, PQ=2PM . Now, using the length of PM, get the length of PQ.
Complete step-by-step answer :
According to the question, we have a circle in which there is a chord PQ. The line segment AM drawn from the center A to the chord PQ such that AM is perpendicular to the chord PQ.
From the figure, we have
The length of the line segment AP = 34 cm …………………………………(1)
The length of the line segment AM = 30 cm …………………………………(2)
In the ΔAMP , we have
AM = Perpendicular = 30 cm ………………………………………….(3)
AP = Hypotenuse = 34 cm …………………………………………..(4)
PM = Base ………………………………………(5)
∠AMP=90∘ ……………………………………….(6)
Since the line segment, AM is perpendicular to the chord PQ so, we can apply the Pythagoras theorem in ΔAMP .
We know the Pythagoras theorem,
(Hypotenuse)2=(Perpendicular)2+(Base)2 ………………………………………………….(7)
Now, from equation (3), equation (4), equation (5), and equation (7), we have
