Question

In fig. $P$ is a point in the interior of a parallelogram ABCD. Show that
(i) $ar(APB) + ar(PCD) = \dfrac{1}{2}ar(ABCD)$
(ii) $ar(APD) + ar(PBC) = ar(APB) + ar(PCD)$

Answer 1

Hint : First of all it is given that the quadrilateral shown in the figure is a parallelogram. Further we will take a triangle and a parallelogram; they have the same base between the parallel lines. Then by using , area of triangle $= \dfrac{1}{2}area$ of parallelogram.

Complete step-by-step answer :

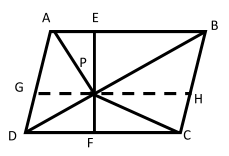
: $ABCD$ is a parallelogram and $P$ is the interior point
To prove (i) ar$(APB) + ar(PCD) = \dfrac{1}{2}ar(ABCD)$
(ii) $ar(APD) + ar(PBC) = ar(APB) + ar(PCD)$
Construction: Draw a line $EF$ through P and parallel to $BC$ and $GH$ through point $P$ and parallel to AB
Proof: Since ABCD is a parallelogram
(i) So, $AB||CD$ (opposite sides of a parallelogram are parallel)
And $AD||BC$
Now, $GH||AB$ and $AB||CD$
Then $AB||GH||CD$
$\therefore ABHG$ is a parallelogram because $AB||GH$ and $GHCD$ is also a parallelogram, because $GH||CD$
Now, in parallelogram $ABHG$ and triangle $APB$ have same base $AB$ and between the same parallel line $AB\,\,and\,\,GH$
$\therefore$ Area $(\Delta APB) = \dfrac{1}{2}area(ABHG)$ ….(i)
As we know that area of a triangle is half of parallelogram if they have the same base and between parallel lines
In parallelogram $GHCD$ and a triangle $DPC$ have the same base $CD$ and between the same parallel line $CD\,\,and\,\,GH$ .
$\therefore ar(\Delta DPC) = \dfrac{1}{2}ar(GHCD)$ ……(ii)
As we know that area of a triangle is half of the parallelogram if they have the same base and between the parallel lines
Adding equation (i) and (ii) we will get
$ar(\Delta APB) + ar(\Delta dpc) = \dfrac{1}{2}ar(ABHG) + \dfrac{1}{2}ar(GHCD)$
$ar(\Delta APB) + ar(\Delta DPC) = \dfrac{1}{2}\left[ {ar(ABHG) + ar(GHCD)} \right]$
$ar(\Delta APB) + ar(\Delta DPC)$ $= \dfrac{1}{2}ar(ABCD)$ …..(iii)
Hence prove (i)
(iii) Now $EF||BC$ (by construction)
And $AD||BC$ (opposite sides of parallelogram are parallel)
So, $EF||BC||AD$
$\therefore AEFD\,\,and\,\,EBCD$ are parallelogram as $EF||AD\,\,and\,\,EF||AC$
Now, triangle $APD$ and a parallelogram $AE$ $FD$ have same base $AD$ and between parallel lines are $AD$ and $EF$ ….(iv)
As we know that area of the triangle is half of the parallelogram if they have the same base between the parallel lines.
Triangle $PBC$ and parallelogram $EFCB$ have same base $BC$ and between parallel lines $EF\,\,and\,\,BC$
$ar(\Delta PBC) = \dfrac{1}{2}AR(EFCB)$ ……(v)
Adding equation (iv) and (v), we have
$ar(\Delta APB) + ar(\Delta PBC) = \dfrac{1}{2}ar(AEFD) + \dfrac{1}{2}ar(EFCB)$
$ar(\Delta APB) + ar(\Delta PBC) = \dfrac{1}{2}ar(AEFD) + ar(EFCB)$
$ar(\Delta APB) + ar(\Delta PBC) = \dfrac{1}{2}ar(ABCD)$ …..(vi)
From equation (iii) and (vi), we will get
$ar(\Delta APB) + ar(\Delta DPC) = ar(\Delta APB) + ar(\Delta PBC)$

Note : Students keep in mind that if a triangle and parallelogram have the same base and between same parallel lines then the area of a triangle is equal to half of the parallelogram.