Question

In fig, CODF is a semicircular loop of a conducting wire of resistance $R$ and radius $r$. It is placed in a uniform magnetic field $B$, which is directed into the page (perpendicular to the plane of the loop). The loop is rotated with a constant angular speed $\omega$ about an axis passing through the centre $O$ and perpendicular to the page. Then the induced current in the wire loop is:

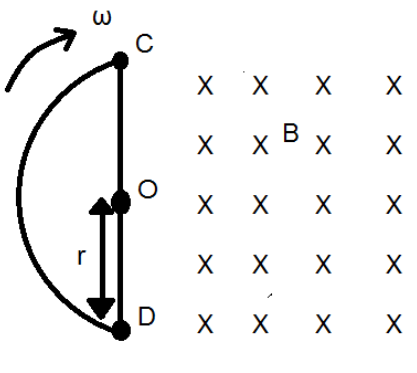
A). 0
B). $\dfrac{B{{r}^{2}}\omega}{R}$
C). $\dfrac{B{{r}^{2}}\omega}{2R}$
D). $\dfrac{B{{r}^{2}}\pi \omega}{R}$

Answer 1

In order to solve this question, we are going to first find the change in the area for a small rotation of the wire through a small angle for a small time, after that the change in flux is calculated from dot product of area and magnetic field and thus, induced emf and current are found.
Formula used: The change in the flux of the magnetic field for a rotation though the area $A$ and the magnetic field$B$is given by:
$d\phi = B \cdot dA$
Induced emf is given by
$e = - \dfrac{{d\phi }}{{dt}}$

Complete step-by-step solution:
Let us consider that the time taken for the wire to rotate through a small angle equal to$d\theta$is $dt$
Now, the change in the area for this much rotation is given by the formula
$A = d\theta \left( {\dfrac{{\pi {r^2}}}{{2\pi }}} \right) = \dfrac{{d\theta }}{2}{r^2}$
Now the change in the flux of the magnetic field for a rotation though the area$A$and the magnetic field$B$is given by:
$d\phi = B \cdot dA$
Putting the values in this equation, we get
$d\phi = B \cdot dA = B\dfrac{{d\theta }}{2}{r^2}$
Now the induced emf is the negative rate of change of the flux,
$e = - \dfrac{{d\phi }}{{dt}}$
Again putting the values in this equation,
$e = - \dfrac{B}{2}\dfrac{{d\theta }}{{dt}}{r^2}$
Now as we know that,
$\dfrac{{d\theta }}{{dt}} = \omega$
Hence by substituting the value of $\dfrac{{d\theta }}{{dt}}$, we get
$e = - \dfrac{B}{2}\omega {r^2}$
Now we know that current induced in a conductor is given by the formula
$i = - \dfrac{e}{R}$
Thus, by substituting we get the induced current in the wire loop as
$i = \dfrac{{B\omega {r^2}}}{{2R}}$
Thus option (c) is correct.

Note: It is important to note that the current produced in a conductor due to change in magnetic flux through the region is called induced current. Magnetic flux is a product of magnetic field and area of Cross section. Like current produced in a generator is induced current. The change in the flux for the rotation is to be found carefully.