Question
Question: In fig. block 1 is placed on block2. Both of them have mass \(1kg\). The coefficients of friction be...
In fig. block 1 is placed on block2. Both of them have mass 1kg. The coefficients of friction between block 1 and 2 are μs=0.75and μk=0.6. The table is frictionless. A force 2p is applied on block 1 to the left, and force P on block 2 on the right. Find the minimum value of P such that sliding occurs between the two blocks.
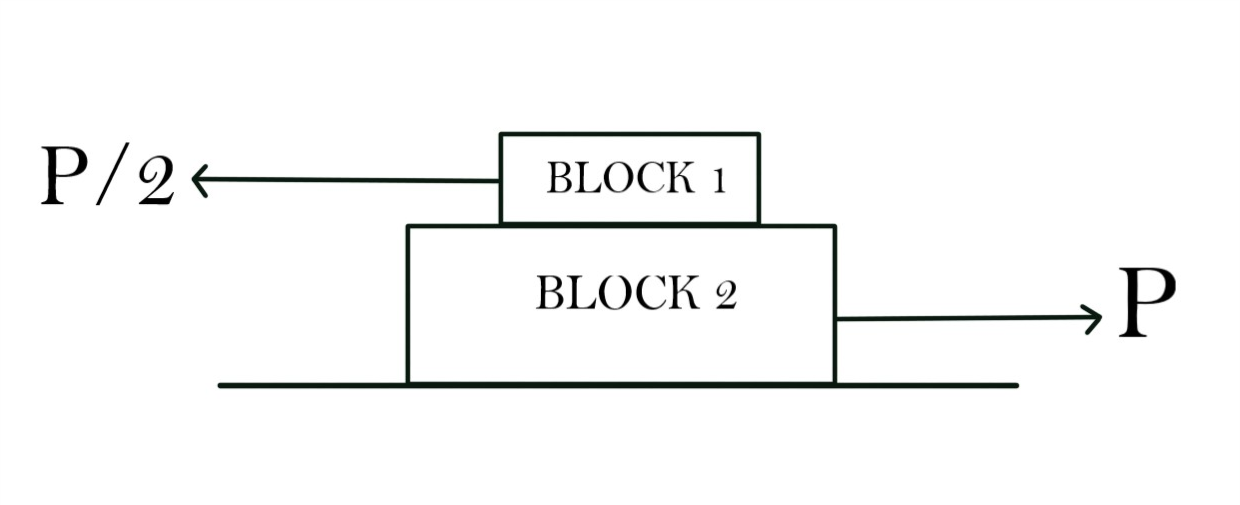
Solution
Hint: Make a free body diagram of both the blocks and balance forces for each of them. They compare both the equations. The friction on each block would be equal and opposite in direction and is equal to the product of coefficient of static friction and mass of block 1.
Complete step-by-step answer:
First, we have to make the free body diagram of both the blocks individually.
Free body diagrams of block 1 and block 2 are given below.
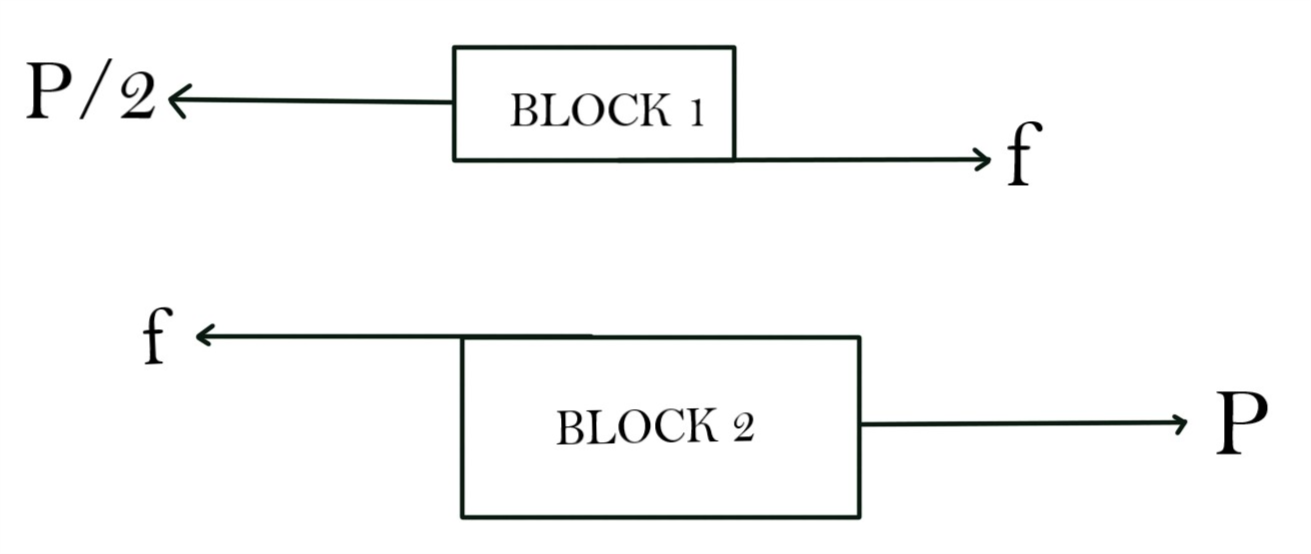
Where f is the force of friction between the two blocks. Here the force of friction on block 1 is to the right because the force of the block is trying to make the block move toward left. Similarly, the force of friction on block 2 is to the left. The force on friction between the two blocks is equal in magnitude because it is an internal force.
We know that,
f=μsmg
f=0.75×1×10 f=7.5N
From the free body diagram of first block, we can conclude:
2P⩾f 2P⩾7.5 P⩾15N
From the free body diagram of second block, we can conclude:
P⩾7.5N
From both the equations, we can conclude that Pshould be greater than 7.5N in order to make the blocks slide.
Additional information: Static friction is the frictional force acting between two surfaces which are attempting to move but are not moving. Kinetic friction is the frictional force acting between two surfaces which are in motion against each other. Static friction is always greater than that of kinetic friction.
Note: In this question, we use static friction instead of kinetic friction because static friction is greater than kinetic friction and the force has to overcome static friction in order to make the blocks slide over each other.
