Question

In Fig.1.35, a uniform bar of length 1 m is supported at its end and loaded by a weight $W$ kgf at its middle. In equilibrium, find the reactions ${R_1}$and ${R_2}$at the ends.

Answer 1

For the bar to be in equilibrium, the net force and torque should become zero (else the bar would become unstable and start to move). So, we can equate the forces and torque such that the net force and net torque would become zero. And deduce the relations.

Complete step by step answer:
As we know, the bar has been loaded by a weight of $W$kgf. Hence the bar would experience a force equivalent to the weight of the load in the downward direction (I.e. towards earth). For the sake of simple calculation, we will consider the centre of the bar to be our origin of the coordinate system, in which we will do our calculation.

X axis shall be along the bar and we will take y axis to be perpendicular to the length of the bar, along the direction of gravity.Hence our coordinate system would be as shown in the figure below.The blue lines represent the coordinate axis, the red lines represent the forces.

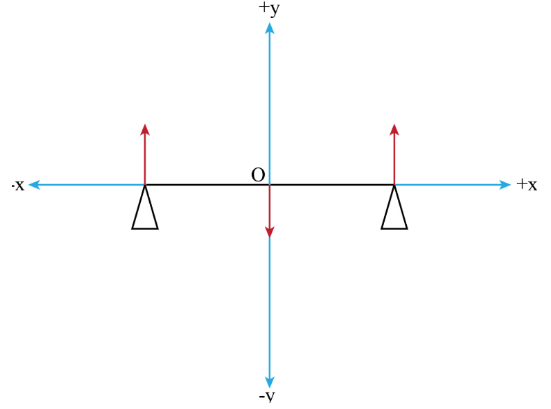
For the system to be in equilibrium the net force acting on the system should be zero.
Let us consider the force along $x$,$y$ , $z$axis to be ${F_x}$,${F_y}$,and${F_z}$respectively.
after analysing the figure, we can understand that there is no force present in the x and z axis,
${F_x} = 0$
${F_z} = 0$
So, the only components of force are present in the $y$direction.
The components of force in $+ y$and $- y$direction will cancel each other.
Here, I have taken a conventional coordinate system where downwards(in the direction of gravity is $- y$and upward is$+ y$. Similarly, towards right is $+ x$and towards left is $- x$.
Forces in $+ y$direction are ${R_1}$and ${R_2}$. And in $- y$direction there is $W$
Total force in $+ y$= total force in $- y$
${R_1} + {R_2} = W$……………… (1)
After being done with the forces we will take the torque into consideration.Torque is the cross product of Force and Radius, or in this case it is the product of the reaction force with the distance perpendicular to it from the centre.As the force is a reaction force it is always perpendicular to the surface which it acts on, and thus the reaction force will always be perpendicular to the bar.

For net torque to become zero, the torque in the clockwise direction should cancel out the torque in the anticlockwise direction.It is important to note that both the reaction forces are positive but the distance which they are being multiplied to are not. One is in the $- x$axis while the other is in the $+ x$.
Thus, writing the equation of the total torque of the bar at equilibrium
${R_1} \times {x_1} + {R_2} \times {x_2} + W \times 0 = 0$……………………………… (2)
Also, we know that ${x_1} = - {x_2}$
And $\left| {{x_1}} \right| = 0.5m$ which is half of the total length (2) becomes
${R_1} \times {x_1} = - {R_2} \times {x_2}$
Or ${R_1} = {R_2}$
Substituting in (1)
$\therefore{R_1} = {R_2} = \dfrac{W}{2}Kgf$

Hence both the reactions are equal to $\dfrac{W}{2}Kgf$.

Note: It is very important to understand the nature of the coordinate system and the signs which you consider on solving the problem. Both reactions are positive, but the perpendicular distance is negative.Also balancing of force does not imply the balancing of torque.