Question

In end on and broadside on position of a deflection magnetometer, if ${{\theta }_{1}}$ and ${{\theta }_{2}}$ are the deflections produced by short magnets at equal distances, then $\dfrac{\tan {{\theta }_{1}}}{\tan {{\theta }_{2}}}$ is
(A) 2:1
(B) 1:2
(C ) 1:1
(D) None of these

Answer 1

The magnetic field is directly proportional to the tan of the angle. And the proportionality constant is the horizontal component of the magnetic field. The horizontal component of earth’s magnetic field is the earth’s magnetic field projection. The horizontal component of earth’s magnetic field can be measured using a compass. The needle of a compass is a small magnet that will always align with an external magnetic field. The opposite poles of the magnet attract and like poles repel.

Complete step by step solution:
$B={{B}_{H}}\tan \theta$
End on position

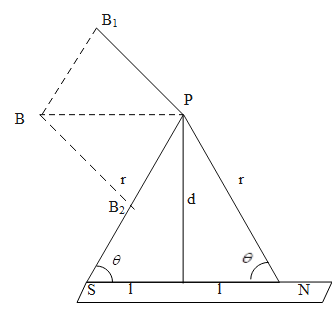
In the end,
${{B}_{1}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{r}^{2}}}$
${{B}_{1}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{\left( d-l \right)}^{2}}}$
which is directly away from N-pole. Since the south pole of the magnet is at a distance r=d+l from P, so magnetic field intensity at P due to S pole is,
${{B}_{2}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{r}^{2}}}$
${{B}_{2}}=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{\left( d+l \right)}^{2}}}$
which is directed to the south pole.
The resultant field is,
$B={{B}_{1}}+\left( -{{B}_{2}} \right)$
$B=\dfrac{{{\mu }_{0}}m}{4\pi }\left[ \dfrac{1}{{{\left( d-l \right)}^{2}}}-\dfrac{1}{{{\left( d+l \right)}^{2}}} \right]$
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{\left( d+l \right)}^{2}}}$
${{B}_{1}}=\dfrac{{{\mu }_{0}}2Md}{4\pi {{\left( {{d}^{2}}-{{l}^{2}} \right)}^{2}}}$
Similarly on the broad side,
${{B}_{2}}=\dfrac{{{\mu }_{0}}M}{4\pi {{\left( {{d}^{2}}+{{l}^{2}} \right)}^{\dfrac{3}{2}}}}$
$\dfrac{\tan {{\theta }_{1}}}{\tan {{\theta }_{2}}}={{B}_{1}}:{{B}_{2}}=2:1$

Thus option (A) is correct.

Additional information:
Magnetic flux density is measured in Teslas. The magnetic flux is the strength of the magnetic lines produced by the magnet.
A magnetic field can be described as an influence of magnetic effect on the moving electric charges. Thus a magnetic field is a vector field. The moving charges or currents produce a magnetic field in the surrounding space. Electrostatic field lines always form closed loops. That is, it starts at a positive charge and terminates at a negative charge. Magnetic field lines always form closed loops. Thus the field lines are circles concentric with the wire.

Note:
Magnetic induction describes a magnetic force on a test object like a small piece of iron in space. The horizontal component of earth’s magnetic field is the earth’s magnetic field projection. The horizontal component of earth’s magnetic field can be used as a compass. The needle of a compass is a small magnet that will always align with an external magnetic field. The opposite poles of the magnet attract and like poles repel.