Question

In each of the following find the value of $k$, for which the points are collinear.
$(i) (7, -2), (5,1), (3,k)$
$(ii) (8,1), (k, -4), (2, -5)$

Answer 1

Here we have to know that the area of triangle is defined as the total region that is enclosed by the three sides of any particular triangle.
The area of the triangle formed by given vertices is equal to zero.
Area of triangle =$\dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
By using the area of the triangle formula and putting it equal to zero.
We will get the value of $k$.

Complete step-by-step answer:
(i). It is given that $A(7, - 2), B(5,1), C(3,k)$

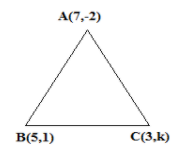
We need to find the value of $k$
First we will find the area of the triangle and then put that equal to zero.
Area of triangle=$= \dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
Here, coordinates are:
${x_1} = 7,{y_1} = - 2$
${x_2} = 5,{y_2} = 1$
${x_3} = 3,{y_3} = k$
Putting the values in the above formula so we get,
∴ Area of triangle, for the given coordinates is
$\Rightarrow \dfrac{1}{2}\left[ {7(1 - k) + 5(k - ( - 2)) + 3( - 2 - 1)} \right] = 0$
Multiply the in between terms, we get
$\Rightarrow \dfrac{1}{2}\left[ {7 - 7k + 5k + 10 - 9} \right] = 0$
On adding the numbers and variables terms we get,
$\Rightarrow \dfrac{1}{2}\left[ {8 - 2k} \right]$
We have to equate that because we have to find the value of $k$
$\Rightarrow 8 - 2k = 0$
In forms of the equation we get,
$\Rightarrow 2k = 8$
Divided the terms we get the value of $k$
$\therefore k = 4$
Hence the value for the $k$ is 4.

(ii). It is given that the points be $P(8,1),Q(k, - 4),R(2, - 5)$

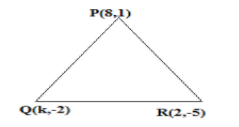
we have to find the value for k.
Since the given points are collinear, it means the area of the triangle formed by them is equal to zero.
On applying the area of triangle formula
∴Area of triangle $= \dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
We have to put area of triangle equals to zero
Here, the coordinates are:
${x_1} = 8,{y_1} = 1$
${x_2} = k,{y_2} = - 4$
${x_3} = 2,{y_3} = - 5$
So, Area of triangle is, and putting it equal to zero
$\Rightarrow \dfrac{1}{2}\left[ {8( - 4 - ( - 5)) + k( - 5 - 1) + 2(1 - ( - 4))} \right] = 0$
On adding the brackets terms and multiply the terms we get,
$\Rightarrow \dfrac{1}{2}\left[ {8 - 6k + 10} \right] = 0$
Adding the two values we get,
$\Rightarrow \dfrac{1}{2}\left[ {18 - 6k} \right] = 0$
We have to equate that because we have to find the value of $k$
$\Rightarrow 18 - 6k = 0$
In the formation of the terms we get,
$\Rightarrow 18 = 6k$
Dividing the terms we get,
$\therefore k = 3$
Hence the value for $k$ is 3.

Note: We must always remember about collinear points and non collinear points as they can come in a handy.
Also, one more thing is to remember that collinear points are the points that lie on the straight line and non collinear are the points that do not lie on a straight line.