Question
Question: In each of the following a force, \(F\) is acting on an object of mass \(M\). The direction of displ...
In each of the following a force, F is acting on an object of mass M. The direction of displacement is from west to east shown by the longer arrow. Observe the diagram carefully and state whether the work done by the force is negative, positive or zero.
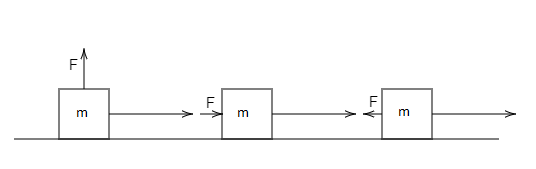
Solution
Hint
The work done by the force can be determined by using the formula which shows the relation between the direction of the force and the direction of the motion of the object and the angle between the direction of motion and the force. By using this the solution can be determined.
The formula which shows the relation between the direction of the force and the direction of the motion of the object and the angle between the direction of motion and the force is given by,
⇒W=FScosθ
Where, W is the work done by the force on the object, F is the force acting on the object, S is the direction of the motion of the object and θ is the angle between the force and the direction of the motion of the object.
Complete step by step answer
Given that, The force is acting on the object is, F
The mass of the object is, M
The work done by the force is given by,
⇒W=FScosθ...................(1)
1. For the first diagram,
The angle between the force and the direction of the motion of the object is, θ=90∘
By substituting the angle between the and the direction of the motion of the object in the equation (1), then
⇒W=FScos90∘
From trigonometry, the value of the cos90∘=0, by substituting this value in the above equation, then
⇒W=FS×0
By multiplying the terms, then
⇒W=0
For the first condition, the work done by the force is zero.
2. For the second diagram,
The angle between the force and the direction of the motion of the object is, θ=0∘
By substituting the angle between the and the direction of the motion of the object in the equation (1), then
⇒W=FScos0∘
From trigonometry, the value of the cos0∘=1, by substituting this value in the above equation, then
⇒W=FS×1
By multiplying the terms, then
⇒W=FS>0
For the second condition, the work done by the force is positive.
3. For the third diagram,
The angle between the force and the direction of the motion of the object is, θ=180∘
By substituting the angle between the and the direction of the motion of the object in the equation (1), then
⇒W=FScos180∘
From trigonometry, the value of the cos180∘=−1, by substituting this value in the above equation, then
⇒W=FS×−1
By multiplying the terms, then
⇒W=−FS
For the third condition, the work done by the force is negative.
Note
From the above three conditions, it is well known that the work done by the force depends on the angle of the force which acts on the object when the application of the force and the direction of motion of the object is the same for all the three conditions.
