Question

In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of $\dfrac{n\lambda}{a}$. Justify this by suitably dividing the slit to bring out the cancellation.

Answer 1

Diffraction is the property of the light where the light encroaches the regions are supposed to be dark. This is observed when the light is passed through a small aperture whose width is comparable to the wavelength of the light.

Formula Used:
$\theta=\dfrac{\lambda}{t}$

Complete step-by-step answer :
Single slit diffraction is observed when the light bends through the small aperture whose width is comparable to the wavelength of the light. This produces a diffraction pattern, with a central maxima and secondary minima. The difference between two consecutive secondary minima gives the secondary maxima.
Consider single silt with an aperture of width $d$ and placed at a distance $L$ from the screen. Let us assume that they are divided into $n$ smaller slits.

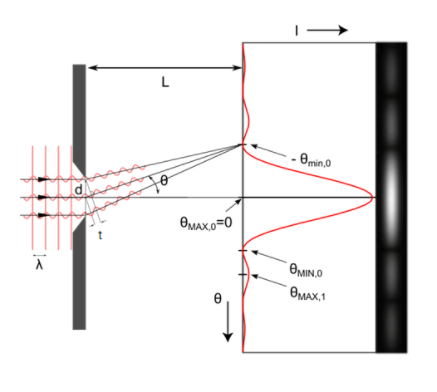
Then the width of $n$ small slits will be $t=\dfrac{d}{n}$
Then the angle of diffraction will be given as $sin\theta=\dfrac{n\lambda}{t}$
For small angles $sin\theta \approx tan\theta\approx \theta$
Then, we can say $\theta=\dfrac{n\lambda}{t}$
The position of central maxima $y=\dfrac{n\lambda L}{t}$
Central maxima is observed at $n=0$ with a width of $2\lambda Lt$ and angular with of $2\theta=2\lambda t$
For secondary destructive interference or for dark fringe $n=..-2,-1,1,2..$
Clearly, $n\neq 0$
Then clearly, the secondary minimum is a value close to zero but never zero.
Then the secondary minima can become zero, only if $t$ tends to be infinitely small.

Note : Students often confuse between diffraction and interference. Diffraction and interference occur simultaneously and hence it is hard to differentiate both by observing the pattern. However, Interference is a property where two coherent sources are used to produce two fringes of different intensity, whereas diffraction is observed when the secondary wavelets that originate from the same wave produce two fringes of different intensity.