Question

In deriving a formula for the combined resistances of three different resistances in series, Kirchhoff’s laws are used. Which physics principle is used in the derivation
a) The conservation of charge
b) The direction of the flow of charge is from negative to positive
c) The potential difference across each resistor is the same
d) The current varies in each resistor, in proportion to the resistance value.

Answer 1

To select the correct alternatives provided to us in the options, we first need to define both the Kirchhoff’s laws. Once we state the Kirchhoff’s laws we will verify what physics principle they are based on. Further, we will see how these laws are used to derive the equivalent resistance in series and accordingly conclude a correct answer among the given options.

Formula used:
$\sum\limits_{i=1}^{N}{{{V}_{N}}}=0$
$I=\sum\limits_{i=1}^{N}{{{I}_{N}}}$
$V=IR$

Complete step-by-step solution:
There are two laws of Kirchhoff’s which are used to determine current and the voltage in the circuit. These laws are as follows.
Kirchhoff’s current law states that current flowing into a node or a junction must be equal to the current flowing out of it. If the current I flows to N junctions than the mathematically this is written as $I=\sum\limits_{i=1}^{N}{{{I}_{N}}}$
Kirchhoff’s second law states that the sum of the voltage (V)around any closed loop in a circuit must be equal to zero. Let us say there are( N-1) resistances in a loop along with a battery, then this can be mathematically be written as $\sum\limits_{i=1}^{N}{{{V}_{N}}}=0$
The first Kirchhoff’s law is based on the conservation of charge i.e. there is no charge lost as the current flows from one to N junctions. We use both these laws to determine the equivalent resistance in series.
Hence, therefore, the correct answer of the above question is option a.

Note: Now since we already know the answer let us understand how these laws are used to determine the equivalent resistance in series.
Before that let us state ohm's law. The current(I) flowing through a resistor(R)is proportional to the potential difference provided the temperature remains the same. Mathematically this law can be written as $V=IR$
Let us consider three resistances i.e. ${{\text{R}}_{\text{1}}}\text{,}{{\text{R}}_{\text{2}}}\text{ and }{{\text{R}}_{\text{3}}}$ all connected in series as shown below to a such that the potential difference across them is V and the current in the circuit be(I).

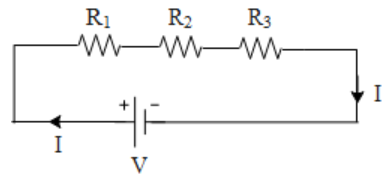
If we apply the Kirchhoff’s second law to the above closed circuit we get, $V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}$ By ohm's law the individual potential differences across the resistors are ${{V}_{1}}={{I}_{1}}{{R}_{1}}$, ${{V}_{2}}={{I}_{2}}{{R}_{2}}$ and ${{V}_{3}}={{I}_{3}}{{R}_{3}}$ Let R be the equivalent resistance of the above circuit. Therefore V can be written as, $V=IR$. If we see the above circuit there is only one path to the flow of current i.e. current does not go through any junctions. Therefore from Kirchhoff’s first law we can say that, $I={{I}_{1}}={{I}_{2}}={{I}_{3}}$ Substituting all the results obtained in the equation of Kirchhoff’s second law we get,
$\begin{aligned} & V={{V}_{1}}+{{V}_{2}}+{{V}_{3}} \\\ & \Rightarrow IR={{I}_{1}}{{R}_{1}}+{{I}_{2}}{{R}_{2}}+{{I}_{3}}{{R}_{\text{3}}}\text{, }\because I={{I}_{1}}={{I}_{2}}={{I}_{3}} \\\ & \Rightarrow IR=I{{R}_{1}}+I{{R}_{2}}+I{{R}_{\text{3}}} \\\ & \Rightarrow R={{R}_{1}}+{{R}_{2}}+{{R}_{\text{3}}} \\\ \end{aligned}$
Therefore we can conclude that the resistance in series gets added up.