Solveeit Logo
Login

Question

Question: In \(\Delta XYZ,\angle XYZ = {90^ \circ },\angle YXZ = {60^ \circ },\angle YZX = {30^ \circ }\) and ...

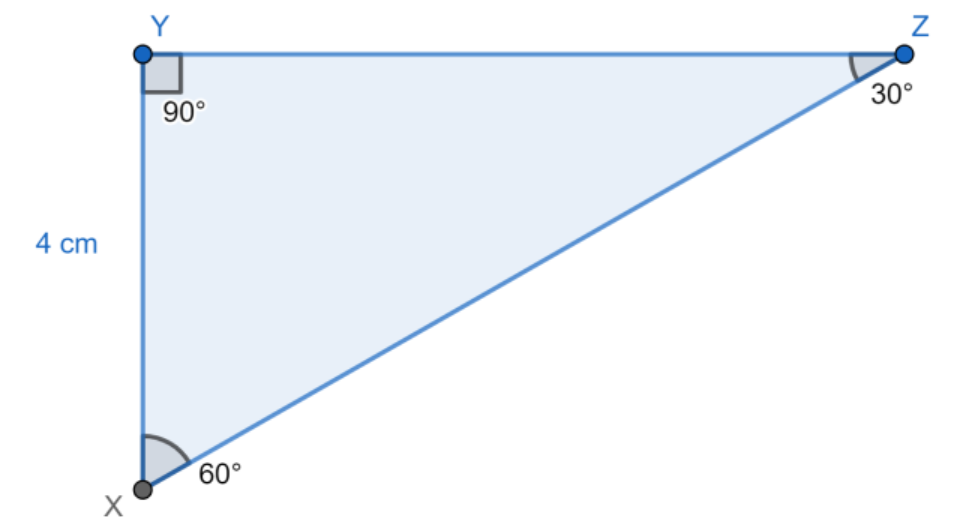
In ΔXYZ,∠XYZ=90∘,∠YXZ=60∘,∠YZX=30∘\Delta XYZ,\angle XYZ = {90^ \circ },\angle YXZ = {60^ \circ },\angle YZX = {30^ \circ } and XY=4XY = 4cm then find XZXZ.

Explanation

Solution

In a right-angled triangle the sine of an angle is the length of the opposite side of an angle divided by the hypotenuse of the triangle. Here we need to calculate the hypotenuse of the triangle. So we should use this formula to calculate the hypotenuse by replacing the sine value and length of the opposite side of the angle. From the trigonometric table, we know that sin⁡30∘=12\sin {30^ \circ } = \dfrac{1}{2}.

Complete step by step solution:
From the figure, we can see ΔXYZ\Delta XYZ is a right-angled triangle because ∠XYZ=90∘\angle XYZ = {90^ \circ }.
Here, ∠XYZ=90∘,∠YXZ=60∘,∠YZX=30∘\angle XYZ = {90^ \circ },\angle YXZ = {60^ \circ },\angle YZX = {30^ \circ } and XY=4XY = 4 cm.
We need to find the value of XZXZ i.e. the value of hypotenuse of the triangle ΔXYZ\Delta XYZ.
Here the base of the triangle is YZYZ and perpendicular is XYXY.
sin⁡∠YZX\sin \angle YZX is the ratio of side XYXYi.e. the perpendicular of the triangle and the hypotenuse of the triangle XZXZ in ΔXYZ\Delta XYZ.
First, we calculate the sine value of ∠YZX\angle YZX. We take the value of sin⁡30∘\sin {30^ \circ }from the trigonometric table.
∴sin⁡∠YZX=sin⁡30∘=12\therefore \sin \angle YZX = \sin {30^ \circ } = \dfrac{1}{2}.
According to the formula of sine of an angle we have:
sin⁡∠YZX=XYXZ\sin \angle YZX = \dfrac{{XY}}{{XZ}}
Taking the unknown value i.e. side XZXZ on the left-hand side of the equation we get:
⇒XZ=XYsin⁡∠YZX\Rightarrow XZ = \dfrac{{XY}}{{\sin \angle YZX}}
Replacing the required values in the above formula we get:
∴XZ=412\therefore XZ = \dfrac{4}{{\dfrac{1}{2}}}
⇒XZ=4×2\Rightarrow XZ = 4 \times 2
⇒XZ=8\Rightarrow XZ = 8 cm
Hence, the required value of the side XZXZ is 88 cm.

Note: One should be well acquainted with the trigonometric table. Calculating the sine of the angle is very important over here. Much redundant information is also given. So choosing the correct information i.e. which angle to use to find the unknown side is very crucial. This method is useful only for right-angled triangles.