Question
Question: In \[\Delta {\text{PQR}}\] , right-angled at \({\text{Q}}\) , \({\text{PR}} + {\text{QR}} = 25{\text...
In ΔPQR , right-angled at Q , PR+QR=25cm and PQ=5cm. Determine the values of sinP , cosP and tanP.
Solution
In this question first we will draw a triangle ΔPQR having Q as a right angle. Now we will find the length of QR with the help of the equation given in the question and Pythagoras theorem. Now, with the help of QR and PR. We will find what is asked in the question.
Complete step-by-step solution:
We know that PQ=5cm (given in the question). Now we have to find the remaining sides of the triangle ΔPQR
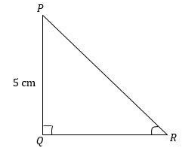
Now, we know that PR+QR=25 (given in the question). Therefore, it can be written as PR=25−QR. From PR=25−QRwe will find the length of QR.
From the figure we can write {\text{P}}{{\text{R}}^{\text{2}}} = {\text{Q}}{{\text{R}}^{\text{2}}} + {\text{P}}{{\text{Q}}^{\text{2}}}\\_\\_\\_(1)
Put the values of PQ and PR in equation (1)
⇒(25−QR)2=QR2+(5)2
Now, simplify the above equation
⇒625−50QR+QR2=QR2+25
Now, cancel the common things
⇒625−50QR−25=0
Now, we can easily find QR
⇒50QR=600 ⇒QR=12
Therefore, we found the length of QR is 12cm . Now, we know that PR=25−QR.
PR=25−QR ⇒PR=25−12=13
From the above calculation we found the length of PR is 13cm.
Now, we know that sinP=hypotenuseopposite side . From the figure we can write sinP=PRQR.
Therefore, we can write sinP=PRQR=1312.
Similarly, we know that cos P=hypotenuseAdjacent side . From the figure we can write cos P=PRPQ.
Therefore, we can write cos P=PRPQ=135.
Similarly, we know that tan P=Adjacent sideopposite side . From the figure we can write tan P=PQQR.
Therefore, we can write tan P=PQQR=512.
Hence, the answers are sinP=1312, cos P=135 and tan P=512.
Note: We can also solve this question by making QR as a subject and then from it we can find PR first. The other important things are the formula of sin , cos and tan which we need to memorize.
sinA = HypotenuseOpposite
cosA = HypotenuseAdjacent
tanA = AdjacentOpposite
cosecA = OppositeHypotenuse
secA = AdjacentHypotenuse
cotA = OppositeAdjacent
