Solveeit Logo
Login

Question

Question: In \(\Delta {\text{ABC}}\), right angled at \({\text{B}}\),\({\text{AB}} = 24\), \({\text{BC}} = 7{\...

In ΔABC\Delta {\text{ABC}}, right angled at B{\text{B}},AB=24{\text{AB}} = 24, BC=7cm{\text{BC}} = 7{\text{cm}}. Determine:
(i) sin⁡A, cos A\sin {\text{A, cos A}}
(ii) sin⁡C, cosC\sin {\text{C, cosC}}

Explanation

Solution

In this question first we will draw a right angle triangle whose sides are AB{\text{AB}} and BC{\text{BC}}. Then, we will find the hypotenuse of the triangle by using Pythagoras theorem. After finding the hypotenuse we will use the formula of sin⁡\sin and cos⁡\cos to find out the answers.

Complete step-by-step solution:
(i) sin⁡A, cos A\sin {\text{A, cos A}}

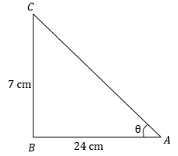
From the figure we can say that AC{\text{AC}} is hypotenuse. AB=24 cm{\text{AB}} = 24\,cm and BC=7 cm{\text{BC}} = 7\,cm is given to us. We have to find AC{\text{AC}}
From the above figure, first we will find the hypotenuse of the right angle triangle. Therefore, from the figure we can write:
AC2=AB2+BC2{\text{A}}{{\text{C}}^{\text{2}}}={\text{A}}{{\text{B}}^{\text{2}}}+{\text{B}}{{\text{C}}^{\text{2}}}
Now, put the value of AB{\text{AB}} and BC{\text{BC}}
⇒(24)2+(7)2=576+49 =625 \Rightarrow {\left( {24} \right)^2} + {\left( 7 \right)^2} = 576 + 49 \\\ = 625
We know that the 625625 is the square of 2525.
⇒AC=625=25\Rightarrow {\text{AC}} = \sqrt {625} = 25
Therefore, AC = 25cm{\text{AC = 25cm}} which is a hypotenuse of the right angle triangle.
Now, we know that sin⁡A=BCAC\sin {\text{A}} = \dfrac{{{\text{BC}}}}{{{\text{AC}}}}. Therefore, we can write sin⁡A=725\sin {\text{A}} = \dfrac{7}{{25}}.
In the same way we know that cos⁡A=ABAC\cos {\text{A}} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}}. Therefore, we can write cos⁡A=2425\cos {\text{A}} = \dfrac{{24}}{{25}}
Therefore, the answers are sin⁡A=725\sin {\text{A}} = \dfrac{7}{{25}} and cos⁡A=2425\cos {\text{A}} = \dfrac{{24}}{{25}}.
(ii) sin⁡C, cosC\sin {\text{C, cosC}}

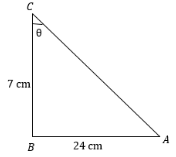
From the figure we can say that AC{\text{AC}} is hypotenuse. AB=24{\text{AB}} = 24 and BC=7cm{\text{BC}} = 7{\text{cm}} is given to us. We have to find AC{\text{AC}}
From the above figure, first we will find the hypotenuse of the right angle triangle. Therefore, from the figure we can write:
AC2=AB2+BC2{\text{A}}{{\text{C}}^{\text{2}}}{\text{=A}}{{\text{B}}^{\text{2}}}{\text{+B}}{{\text{C}}^{\text{2}}}
Now, put the value of AB{\text{AB}} and BC{\text{BC}}
⇒(24)2+(7)2=576+49 =625 \Rightarrow {\left( {24} \right)^2} + {\left( 7 \right)^2} = 576 + 49 \\\ = 625
We know that the 625625 is the square of 2525.
⇒AC=625=25\Rightarrow {\text{AC}} = \sqrt {625} = 25
Therefore, AC = 25cm{\text{AC = 25cm}} which is a hypotenuse of the right angle triangle.
Now, we know that sin⁡C=ABAC\sin {\text{C}} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}}. Therefore, we can write sin⁡C=2425\sin {\text{C}} = \dfrac{{24}}{{25}}
In the same way we know that cos⁡C=BCAC\cos {\text{C}} = \dfrac{{{\text{BC}}}}{{{\text{AC}}}}. Therefore, we can write cos⁡C=725\cos {\text{C}} = \dfrac{7}{{25}}.
Therefore, the answers are sin⁡C=2425\sin {\text{C}} = \dfrac{{24}}{{25}} and cos⁡C=725\cos {\text{C}} = \dfrac{7}{{25}}.

Note: The most important thing in the question is the diagram. So just try to draw a diagram first in this type of question. We also need to memorize the formula for sin⁡\sin and cos⁡\cos . The other important thing is where we are taking that θ\theta because it will help in finding sin⁡\sin and cos⁡\cos . So be careful about these things.