Question

In $\Delta PQR$, right angled at $Q$, $PQ=4\,cm$ and $RQ=3\,cm$. Find the values of $\sin P$, $\sin R$

Answer 1

Hint: We will first draw the figure from the given details in the question and then we will apply the Pythagoras theorem to find the value of the missing side. And after this we will see the point from which we need to find the values and according to that we will select our perpendicular and hypotenuse.

Complete step-by-step answer:
Before proceeding with the question we should know the concept of Pythagoras theorem and right angled triangle.
A Right-angled triangle is one of the most important shapes in geometry and is the basics of trigonometry. A right-angled triangle is the one which has 3 sides, “base” “hypotenuse” and “height” with the angle between base and height being 90 degrees.
Pythagora's theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90 degree.
So we will first draw the figure from the given details in the question.

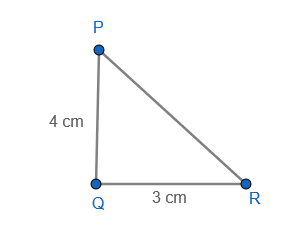
Now we will use Pythagoras theorem and from the figure we get,
$\Rightarrow P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}........(1)$
Now substituting the known values in equation (1) we get,
$\Rightarrow P{{R}^{2}}={{4}^{2}}+{{3}^{2}}........(2)$
Now squaring the terms in the right hand side of the equation (2) and then adding we get,
$\Rightarrow P{{R}^{2}}=16+9=25........(3)$
Now taking the square root on both sides in equation (3) we get,
$\Rightarrow PR=5........(4)$
From the figure we can see that sin P is QR divided by PR. Hence using this information we get,
$\Rightarrow \sin P=\dfrac{perpendicular}{hypotenuse}=\dfrac{QR}{PR}=\dfrac{3}{5}$
Also from the figure we can see that sin R is PQ divided by PR. Hence using this information we get,
$\Rightarrow \sin R=\dfrac{perpendicular}{hypotenuse}=\dfrac{PQ}{PR}=\dfrac{4}{5}$
Hence the value of $\sin P$ is $\dfrac{3}{5}$ and the value of $\sin R$ is $\dfrac{4}{5}$.

Note: Remembering the basic definitions of sin, cos and tan is the key here. Also we should know the Pythagoras theorem and the properties of right angled triangles to solve this question. We in a hurry can make a mistake in substituting the values as we may substitute base in place of hypotenuse or vice-versa and hence we need to be careful while doing this step.