Question

In $\Delta ABC$, $\text{AB}=6\sqrt{3}\text{ cm}$, $\text{AC}=12\text{ }cm$ and $\text{BC}=6\text{ }cm$, then find the measure of $\angle B$.

Answer 1

To find the measure of the angle by using the sides of the triangle, we use the method of trigonometric identities.

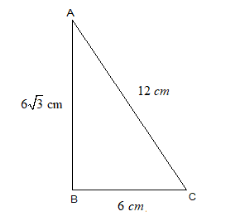
For this question, where both the opposite and adjacent are known the trigonometric identity formula we use:
$\tan \left( \theta \right)=\dfrac{Opp.}{Adj.}$
where $Opp.$ is short for opposite or height of the triangle, $Adj.$ is short for adjacent or base of the triangle and $\theta \ is \\\angle B$.

Complete step-by-step answer:
We place the values of the triangle in the formula of the tangent trigonometric identity and that is:
$\angle B=\tan \left( \theta \right)=\dfrac{Opp.}{Adj.}$
$\tan \left( \theta \right)=\dfrac{AB}{BC}$
Now, $\text{AB}=6\sqrt{3}\text{ cm}$ and $\text{BC}=6\text{ }cm$.
$\tan \left( \theta \right)=\dfrac{6\sqrt{3}}{6}$
$\tan \left( \theta \right)=\sqrt{3}$
Now, if we do inverse of the tangent value that shift $tan$ to the other side we get:
$\angle B=\theta ={{\tan }^{-1}}\sqrt{3}$
The angular value of ${{\tan }^{-1}}\sqrt{3}$ is also known as ${{90}^{\circ }}$.

Hence, the $\angle B={{90}^{\circ }}$.

Note: Another method to find the value of $\angle B$ is by equating the square of the sum of height and base of the triangle with the square of the hypotenuse of the triangle. If both the sum and the hypotenuse squares have equal value i.e. $\left( A{{B}^{2}}+B{{C}^{2}} \right)=\left( A{{C}^{2}} \right)$ or their division $\dfrac{\left( A{{B}^{2}}+B{{C}^{2}} \right)}{\left( A{{C}^{2}} \right)}$ is equal to $1$. Then the angle supporting the base and height is always ${{90}^{\circ }}$ or a right angle triangle.