Question

In $\Delta ABC$, right angled at B, $AB=5cm$ and $\angle ACB={{30}^{\circ }}$. Determine lengths of the sides BC and AC.

Answer 1

Hint:The question has given a right angled triangle, one side and an angle. So, using trigonometric ratios we can find the other sides of the triangle. As length of AB is given so applying $\sin {{30}^{\circ }}=\dfrac{AB}{AC}$ we can get the value of AC. Now, if we can use $\tan {{30}^{\circ }}=\dfrac{AB}{BC}$ then we can find the length of BC.

Complete step-by-step answer:
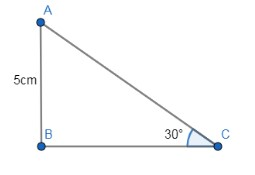
The figure below describes, a $\Delta ABC$ right angled at B and length of $AB=5cm$. It is also given that$\angle ACB={{30}^{\circ }}$.

Using trigonometric ratios,
$\sin \theta =\dfrac{P}{H}$
In the above equation, P stands for perpendicular or the side just opposite to angle θ and H stands for hypotenuse of the right $\Delta ABC$ .
And$\tan \theta =\dfrac{P}{B}$
In the above equation, P stands for perpendicular or the side just opposite to angle θ and B stands for the base (or the side other than perpendicular) of the right $\Delta ABC$ .
In right $\Delta ABC$,
It is given that:
$AB=5cm$
$\angle ACB={{30}^{\circ }}$.
$\sin {{30}^{\circ }}=\dfrac{AB}{AC}$
It can infer from the given figure that AB is the perpendicular and AC is the hypotenuse of the $\Delta ABC$.
$\begin{aligned} & \sin {{30}^{\circ }}=\dfrac{5}{AC} \\\ & \Rightarrow \dfrac{1}{2}=\dfrac{5}{AC} \\\ & \Rightarrow AC=10 \\\ \end{aligned}$
Hence, the length of AC is equal to 10cm.
$\tan {{30}^{\circ }}=\dfrac{AB}{BC}$
It can infer from the given figure that AB is the perpendicular and BC is the base of the $\Delta ABC$.
$\begin{aligned} & \tan {{30}^{\circ }}=\dfrac{5}{BC} \\\ & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{5}{BC} \\\ & \Rightarrow BC=5\sqrt{3} \\\ \end{aligned}$
Hence, length of BC is equal to $5\sqrt{3}$.
Hence, length of AC = 10 cm and length of $BC=5\sqrt{3}$ .

Note: You can check whether the lengths of AC and BC that you are getting is correct or not by satisfying these values in the Pythagoras theorem which is applied on $\Delta ABC$.
In $\Delta ABC$,
$\begin{aligned} & A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} \\\ & {{\left( 10 \right)}^{2}}={{\left( 5 \right)}^{2}}+{{\left( 5\sqrt{3} \right)}^{2}} \\\ \end{aligned}$
$L.H.S=100$
$R.H.S=25+75=100$
From the above calculation, L.H.S = R.H.S. Hence the lengths of the triangle are successfully satisfied Pythagoras theorem.