Solveeit Logo
Login

Question

Question: In \(\Delta ABC\), if\(M\)is the midpoint of side BC, then\(A{B^2} + A{C^2} = 2A{M^2} + 2B{M^2}\)...

In ΔABC\Delta ABC, ifMMis the midpoint of side BC, thenAB2+AC2=2AM2+2BM2A{B^2} + A{C^2} = 2A{M^2} + 2B{M^2}

Explanation

Solution

Since the question is given in terms of squares of sides, it would be better to approach this question by Pythagoras theorem. We need to have a right angled triangle to use Pythagoras theorem. So we will construct a perpendicular to make the question easy.

Complete step by step solution:
We have to prove
AB2+AC2=2AM2+2BM2A{B^2} + A{C^2} = 2A{M^2} + 2B{M^2}
As explained in the hint, draw a perpendicular from A on BC
⇒AD⊥BC\Rightarrow AD \bot BC
InΔABC\Delta ABC, it is also given that, MMis the midpoint of sideBCBC
⇒BM=MC\Rightarrow BM = MC

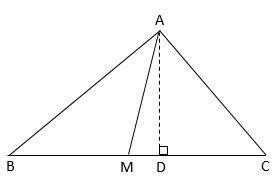
By Pythagoras theorem, in ΔABC\Delta ABC
AB2=AD2+BD2A{B^2} = A{D^2} + B{D^2} and AC2=AD2+DC2A{C^2} = A{D^2} + D{C^2}
Adding the two equations above, we get
AB2+AC2=AD2+BD2+AD2+DC2A{B^2} + A{C^2} = A{D^2} + B{D^2} + A{D^2} + D{C^2} . . . (1)
Now we will rearrange the above equation in such a way that we could substitute the terms that our proof requires.
For that, use
BD=BM+MDBD = BM + MD and DC=MC−MDDC = MC - MD
Hence, equation (1) becomes
AB2+AC2=AD2+(BM+MD)2+AD2+(MC−MD)2A{B^2} + A{C^2} = A{D^2} + {(BM + MD)^2} + A{D^2} + {(MC - MD)^2}
By using the formula (a+b)2=a2+b2+2ab{(a + b)^2} = {a^2} + {b^2} + 2ab and (a−b)2=a2+b2−2ab,{(a - b)^2} = {a^2} + {b^2} - 2ab,we can simplify the above equation as
AB2+AC2=AD2+BM2+MD2+2BM×MD+AD2+MC2+MD2−2MC×MDA{B^2} + A{C^2} = A{D^2} + B{M^2} + M{D^2} + 2BM \times MD + A{D^2} + M{C^2} + M{D^2} - 2MC \times MD
Rearranging the above equation, we get
AB2+AC2=AD2+MD2+BM2+2BM×MD+AD2+MD2+MC2−2MC×MDA{B^2} + A{C^2} = A{D^2} + M{D^2} + B{M^2} + 2BM \times MD + A{D^2} + M{D^2} + M{C^2} - 2MC \times MD
Now, in ΔADM,\Delta ADM,by Pythagoras theorem, we get
AD2+MD2=AM2A{D^2} + M{D^2} = A{M^2}
⇒AB2+AC2=AM2+BM2+2BM×MD+AM2+MC2−2MC×MD\Rightarrow A{B^2} + A{C^2} = A{M^2} + B{M^2} + 2BM \times MD + A{M^2} + M{C^2} - 2MC \times MD
Now, since, BM=MCBM = MC, we can rearrange the above equation as
⇒AB2+AC2=2AM2+BM2+2BM×MD+BM2−2BM×MD\Rightarrow A{B^2} + A{C^2} = 2A{M^2} + B{M^2} + 2BM \times MD + B{M^2} - 2BM \times MD
Simplifying it, we get
AB2+AC2=2AM2+2BM2A{B^2} + A{C^2} = 2A{M^2} + 2B{M^2}
Hence, it is proved that AB2+AC2=2AM2+2BM2A{B^2} + A{C^2} = 2A{M^2} + 2B{M^2}
Additional information:
According to Pythagoras theorem, in a right angled triangle, the sum of squares of two adjacent sides is equal to the square of the hypotenuse.
Mathematically, in a right angle triangle, ABC, right angled at B.

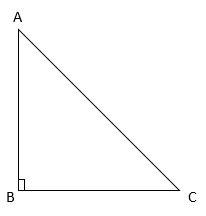
AB2+BC2=AC2A{B^2} + B{C^2} = A{C^2}

Note: Simplest way to solve such a question is to use an approach that uses the information given in the question. This way, it becomes easy to reach the solution in less time. Having a foresight of using a proper construction whenever required can be very helpful in the long run.