Question
Question: In \(\Delta ABC\), if \(\angle A = {90^ \circ }\) and \(AD \bot BC\), then the correct statement is ...
In ΔABC, if ∠A=90∘ and AD⊥BC, then the correct statement is
- AD2=(BD)(DC)
- AB2=BC×BD
- AC2=BC×DC
Solution
After drawing a perpendicular from A, we get two triangles, we will first prove ∠CAD=∠B using properties of triangle. Then, we will find the value of tanB and tan∠CAD from the triangles and then will equate these values to get the desired result.
Complete step-by-step answer:
First of all, let us draw the figure of the given statement. △ADB and CDA.
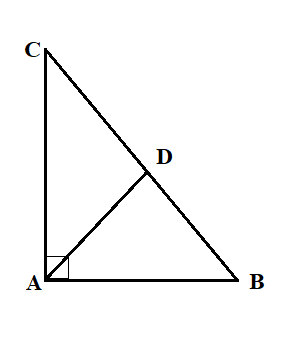
Here, ∠A=90∘ and AD⊥BC.
In △ABC, ∠A+∠B+∠C=180∘ using angle sum property.
Then,
90∘+∠B+∠C=180∘ ⇒∠B=90∘−∠C
In △CAD,
∠ADC+∠CAD+∠ACD=180∘ ⇒90∘+∠CAD+∠ACD=180∘ ⇒∠CAD+∠C=90∘ ⇒∠CAD=90∘−∠C
Hence, ∠CAD=∠B
We will find the required result using trigonometry.
As we know that tanθ=BaseOpposite
Now, in △ADB, we will find the value of tanB using trigonometry.
tanB=BDAD eqn. (1)
Also, we can find the value of tanB, from CDA
tan∠CAD=ADCD
tanB=ADCD eqn. (2)
From equation (1) and (2), we will get,
BDAD=ADCD
On cross-multiplying the above equation, we will get,
AD×AD=CD×BD ⇒AD2=BD×CD
Hence, option A is correct.
Note: Students must know the trigonometric ratios, like sinθ=HypotenuseOpposite, cosθ=HypotenuseBase and tanθ=BaseOpposite. We can also do this question by applying Pythagoras theorem in the right triangles, △ADC and △ADB.
