Question

In $\Delta ABC$, circumradius is 3 and inradius is 1.5 units, then the value of $a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right)$is
A. $5\sqrt 3$
B. $7\sqrt 3$
C. $13\sqrt 3$
D. None of these

Answer 1

First of all, find the ratio of the circumradius and inradius of the given triangle to know whether it is an equilateral triangle or not. If it is an equilateral triangle then all the angles in the triangle are equal and thus the sides. So, use this concept to reach the solution of the given problem.

Complete step by step answer:
Given circumradius of $\Delta ABC$ is $R = 3$
Inradius of $\Delta ABC$ is $r = 1.5$
Now consider the ratio of circumradius and inradius i.e., $R:r = 3:1.5 = 2:1$
We know that if the ratio of circumradius and inradius of a triangle is $2:1$, then the triangle is an equilateral triangle.
So, $\Delta ABC$ is an equilateral triangle i.e., all the three angles are equal to ${60^0}$ as shown in the below figure.

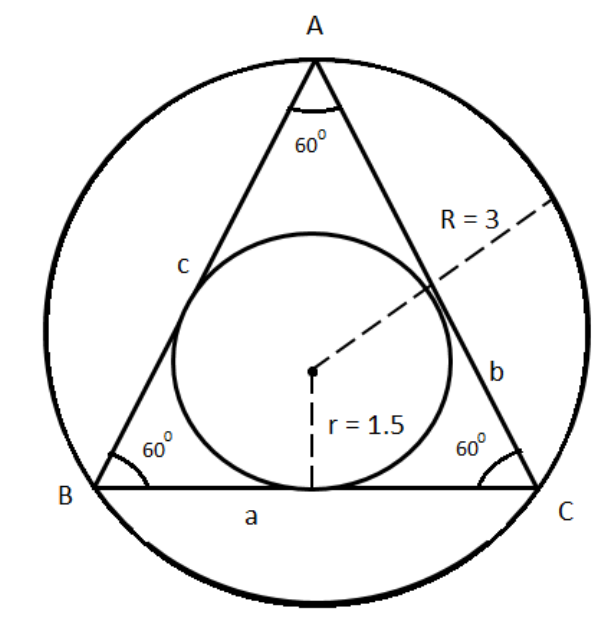
As $\Delta ABC$ is an equilateral triangle it must satisfy that $a = b = c = 2R\sin \dfrac{\pi }{3} = R\sqrt 3$
Now, consider $a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right)$

$$\Rightarrow a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right) = R\sqrt 3 {\cot ^2}\left( {\dfrac{\pi }{3}} \right) + {\left( {R\sqrt 3 } \right)^2}{\cot ^3}\left( {\dfrac{\pi }{3}} \right) + {\left( {R\sqrt 3 } \right)^3}{\cot ^4}\left( {\dfrac{\pi }{3}} \right) \\\ \Rightarrow a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right) = \sqrt 3 R{\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2} + 3{R^2}{\left( {\dfrac{1}{{\sqrt 3 }}} \right)^3} + 3\sqrt 3 {R^3}{\left( {\dfrac{1}{{\sqrt 3 }}} \right)^4} \\\ \Rightarrow a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right) = \dfrac{{\sqrt 3 R}}{3} + \dfrac{{3{R^2}}}{{3\sqrt 3 }} + \dfrac{{3\sqrt 3 {R^3}}}{9} \\\ \Rightarrow a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right) = \dfrac{R}{{\sqrt 3 }} + \dfrac{{{R^2}}}{{\sqrt 3 }} + \dfrac{{{R^3}}}{{\sqrt 3 }} \\\ \Rightarrow a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right) = \dfrac{3}{{\sqrt 3 }} + \dfrac{{{{\left( 3 \right)}^2}}}{{\sqrt 3 }} + \dfrac{{{{\left( 3 \right)}^3}}}{{\sqrt 3 }}{\text{ }}\left[ {\because R = 3} \right] \\\ \therefore a{\cot ^2}\left( A \right) + {b^2}{\cot ^3}\left( B \right) + {c^3}{\cot ^4}\left( C \right) = \dfrac{{3 + 9 + 27}}{{\sqrt 3 }} = \dfrac{{39}}{{\sqrt 3 }} = 13\sqrt 3 \\\$$

So, the correct answer is “Option C”.

Note: If the ratio of circumradius and inradius of a triangle is equal to $2:1$, then that triangle is an equilateral triangle in which all the sides and the angle are equal. Circumradius is defined as the radius of that circle which circumscribes the triangle and the inradius is defined as the radius of the circle which is inscribed in the triangle.