Question
Question: In circle \(O\), \(\overline{AOB}\bot \overline{COD}\). Find m arc \(AC\) and m arc \(ADC\). 
Solution
Hint: To find m arc AC and m arc ADC, we have to find the angle subtended by the arc AC and the arc ADC on the centre of the circle. To find this angle, we will use the information given in the question i.e. AOB⊥COD.
Complete step by step answer:
It is given in the question that AOB⊥COD and A,B,C,D lies on the circumference of the circle which has its centre at point O.
Let us consider the figure given in the question,
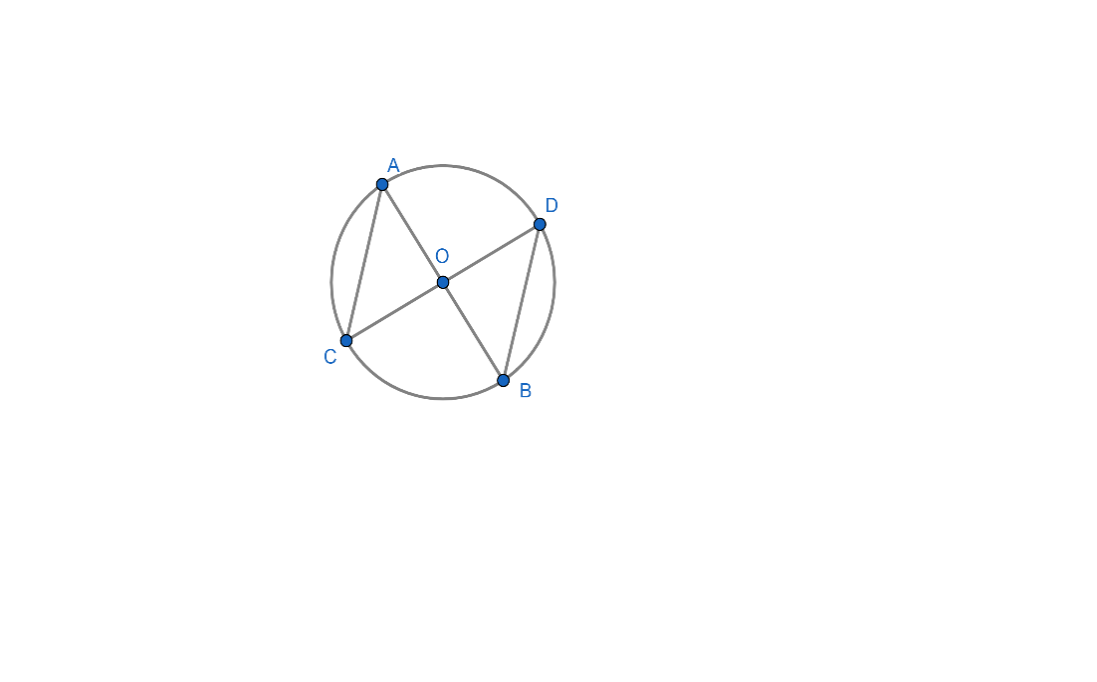
Since it is given that AOB⊥COD, we get
∠AOC=∠AOD=∠DOB=∠BOC=90∘................(i)
In the question, we are required to find m arc AC.
We know that m arc AC is a representation of degree measure of arc AC. This states that the degree measure m arc AC = ∠AOC.
From (i) , we have
∠AOC=90∘
So, we get the degree measure of arc AC=90∘.
Hence, we obtain m arc AC = 90∘.
In the question, we are also required to find m arc ADC.
m arc ADCrepresents the degree measure of arc ADC.
Degree measure of ADC will be equal to the sum of degree measure of arc AOD, arc DOB and arc BOC. This means m arc ADC can be given by
m arc ADC = ∠AOD+∠DOB+∠BOC...............(ii)
From equation (i), we have
∠AOD=∠DOB=∠BOC=90∘
Substituting ∠AOD=∠DOB=∠BOC=90∘ from equation (i) in equation (ii), we get
m arc ADC = 90∘+90∘+90∘.
Hence, we have m arc ADC = 270∘.
So, the degree measures of the arcs AC and ADC are obtained as m arc AC = 90∘ and m arc ADC = 270∘.
Note: There is a possibility that one might make a mistake while calculating m arc AC. One may find out m arc AC as the angle subtended by the major arc AC on the centre of the circle. But since nothing is mentioned in the question, by default, one might consider m arc AC as the angle subtended by the minor arc AC on the centre of the circle.
