Question

In case of concave mirror, the minimum distance between a real object and its real image is:
A) $f$
B) $2f$
C) $4f$
D) zero

Answer 1

In case of a concave mirror, there are 6 cases of position of object with respect to which the position of image varies. Study all the 6 cases to find the minimum distance between a real object and its real image.

Complete step by step solution:
For a concave mirror, there are 6 positions of the object for which ray diagrams can be made, each one resulting in a different position of the image, and different distance between the image and the object.
However, out of these 6 cases, in 1 case, when the object is between $F$ and $O$ of the mirror, the image formed is virtual. Since the distance between a real object and a real image is asked in the question, we will neglect this case and only focus on the other 5 cases.

Case I: When object is at infinity
In this case, two rays emerge from infinity towards the mirror. Both are parallel to the concave mirror. They both get reflected and pass through the focus after reflection. The reflected rays meet at focus. Hence, the image is formed at focus.
Distance between object and image $= \infty - f = \infty$

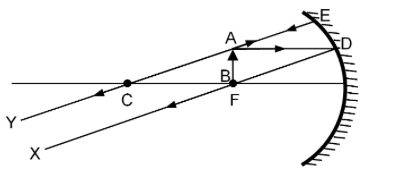
Case II: When object is beyond $C$
In this case, rays emerge from the top of the object. One ray passes parallel to the principal axis and gets reflected through focus of the mirror. Another ray passes through the centre of curvature of the mirror and retraces its path after reflection. These reflected rays meet at a point between $F$ and $C$ of the mirror and below the principal axis. Hence, the image is formed between $F$ and $C$ .
Distance between object and image is approximately between $f$ and $2F$

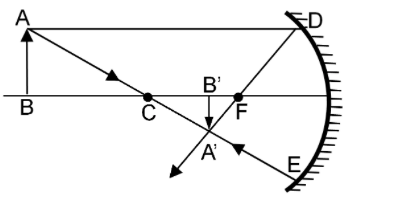
Case III: When the object is at $C$
In this case, rays emerge from top of the object. One ray passes parallel to the principal axis and gets reflected through focus of the mirror. Other rays pass through the focus of the mirror and travel parallel to the principal axis after reflection. These reflected rays meet at $C$ of the mirror and below the principal axis. Hence, the image is formed at $C$ .
Distance between object and image is zero.

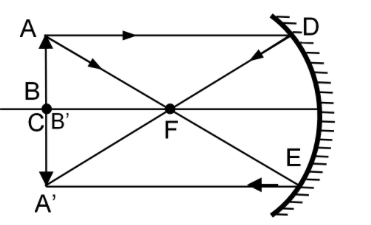
Case IV: When the object is between $F$ and $C$
In this case, rays emerge from top of the object. One ray passes parallel to the principal axis and gets reflected through focus of the mirror. Other rays pass through the focus of the mirror and travel parallel to the principal axis after reflection. These reflected rays meet at a point beyond $C$ of the mirror and below the principal axis. Hence, the image is formed beyond $C$ .
Distance between object and image is approximately equal to $f$ .

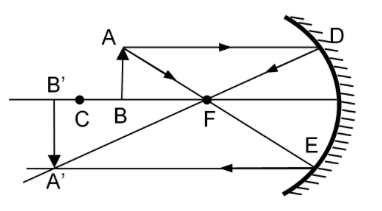
Case V: When the object is at $F$
In this case, rays emerge from the top of the object. One ray passes parallel to the principal axis and gets reflected through focus of the mirror. Other rays appear to have passed through the centre of curvature of the mirror and retraces its path after reflection. These reflected rays do not meet anywhere for a long time. It is assumed that the image will be formed at infinity.
Distance between object and image $= \infty - f = \infty$

After studying all these cases we come to the conclusion that the minimum distance between a real object and its real image is zero. This is the case where the object is at $C$.

Note: The last case is the one where the object is kept between $F$ and $O$ of the mirror. This forms a virtual image behind the mirror. This is the only case a virtual image is formed by a concave mirror. Virtual image in case of concave mirror is only possible if the object is placed between the pole and focus.