Question

In case of a Van de Graff generator, the breakdown field of air is:
A). $2 \times 10^{8}\;Vm^{-1}$
B). $3 \times 10^{6}\;Vm^{-1}$
C). $2 \times 10^{-8}\;Vm^{-1}$
D). $3 \times 10^{4}\;Vm^{-1}$

Answer 1

Note that the breakdown field of air is entirely an empirical quantity, so it cannot be obtained via theoretical calculations. Now, we know that air is an insulator and acts like a dielectric. But when a suitable high voltage is applied to it, it breaks its insulative properties and becomes conductive, and allows the electric charges to pass through it along its field lines. The electric field as a result of this breakdown is called the breakdown field. In such a case, determine what its value could be.

Complete step-by-step solution:
We know that a Van de Graff generator is basically an electrostatic generator which accumulates electric charges on a hollow metal shell by using an internally moving belt and is used to create very high electric potentials and high voltage direct current. Let us begin by looking at how it works.

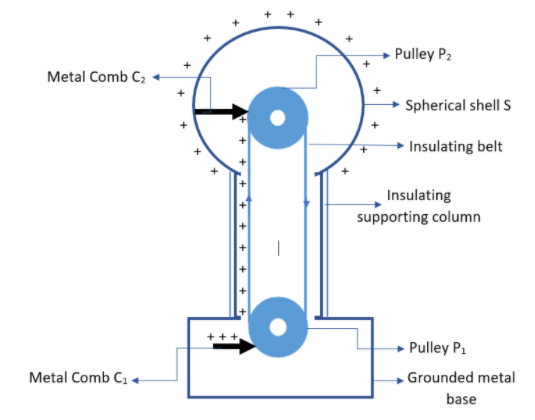
A simple Van De Graff generator consists of an insulating belt usually made of rubber that runs over two moving pulleys $P_1$ and $P_2$, with the entire setup enclosed in a hollow spherical shell$\;S$ and an insulating column grounded at a metal base as shown in the figure. The metal comb $C_1$ is given a high positive potential. Its pointed tip discharges the positive charges onto the belt. The belt carries the positive charges upwards where it passes close to the metal comb $C_2$. These positive charges induce a negative charge on the tip of the comb $C_2$ due to which an equal positive charge is induced at the farther end of $C_2$. This farther end is connected to the hollow spherical shell$\;S$ and the induced positive charges get transferred and distributed over the surface of the spherical shell. The negative charge induced on the tip of $C_2$ gets discharged onto the belt carrying the positive charges, thereby neutralizing the belt as it passes over $P_2$, making it ready to receive the positively charged wind from comb $C_1$ again. This process is repeated multiple times until the electrical potential of the shell reaches several million volts. The shell stores the charges on its outer surface until discharged either by breakdown of the surrounding air as a spark, or by conduction to an adjacent earthed object.
Now, we know that air is normally an excellent insulator. However, when it is stressed by a sufficiently high voltage, it can begin to break down and become partially conductive. This voltage is called the breakdown voltage of air, and the resultant electric field that it arises from is called the breakdown field. This breakdown field, at normal temperature and pressure, is empirically found to be $3 \times 10^{6}\;Vm^{-1}$, which means that 1 metre of air carries a potential of 3 megavolts.
Therefore, the correct choice would be B. $3 \times 10^{6}\;Vm^{-1}$

Note: The voltage produced by most open-air Van de Graff machines are limited by arcing and corona discharge to about 5 megavolts. However, when placed in pressurized tanks of insulating gases, they can achieve potentials as high as 25 megavolts. Arcing is the phenomenon by which charges are able to jump through insulators or dielectrics by breaking them down, whereas corona is the electrical discharge caused by the ionization of the dielectric surrounding the conductor. Thus, arcing entails electrical discharge via flow of electrons, whereas corona entails electrical discharge via flow of ions.