Question

In case of a concave mirror, when the object is situated at the principal focus, then the image formed:
A). Is real and inverted
B). Is of infinite size
C). Lies at infinity
D). Has all properties mentioned above

Answer 1

Try to geometrically determine how the ray diagram for such a situation would look. Start off with the fact that a concave mirror has its reflecting curved surface bent inwards, away from the object. Then use the fact that the incidence and reflected angles are equal about the normal to the mirror surface to trace out two rays from the top of the object, one parallel to the principal axis that is reflected off through the focus and the other passing through the centre of curvature of the mirror. This will give you a clear picture of what the image will look like, from which you can deduce the correct option.

Complete step-by-step solution:
Let us begin by understanding what a concave mirror is and how it works.
A concave mirror or a converging mirror is a curved mirror whose reflecting surface is recessing inwards, away from the incident light. Light rays converge at a focus point when they strike the mirror surface and get reflected back from the reflecting concave surface. This happens because of the differential reflection of light rays at different angles since the normal to the mirror is different at each point on the mirror, owing to its curvature.
Concave mirrors can produce both real and virtual images. They can be upright (if virtual) or inverted (if real). They can be behind the mirror (if virtual) or in front of the mirror (if real). They can also be magnified, minified or the same size as the object.
In any case, we can determine the position of the image with respect to the object by employing the method of ray tracing to trace out the emergent ray path, and consequently the image location and size.

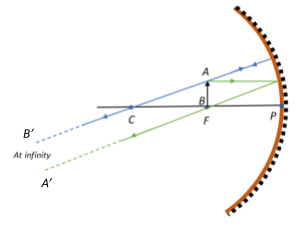
We first begin by drawing a ray from the top of the object to the mirror in such a way that the ray passes through the centre of curvature C of the mirror. We then draw a second ray from the top of the object that is parallel to the principal axis of the mirror, which gets reflected when it strikes the mirror surface in such a way that the reflected ray passes through the focal point of the lens. Usually, the point at which these two rays meet would correspond to the nature of the image and where it’s formed, but we see that the two emergent rays are in fact parallel to each other. This can only mean that the image is formed at infinity, where we assume it converges in space.
Now, since the image is formed on the same side of the mirror as the object, the image is real.
Additionally, from the ray diagram, we see that the image will be flipped upside down at infinity, this means that the image is inverted.
Additionally, since there is a degree of uncertainty as to how large or small the image will be, we can assume that the image will be highly magnified since the rays do not converge as far as we can observe. Thus, we can say that the image is of infinite size.
Therefore, the correct choice would be D. Has all properties mentioned above

Note: It is important to understand that the above conclusion was deduced from a hypothetical approach to image formation. However, in reality, when the object is located at the focal point, there is no location in space at which an observer can perceive the convergence or divergence of emergent rays resulting in image formation. Thus, the results of such a ray diagram can realistically be interpreted by stating that when the object is located at the focal point of a concave mirror, no observable image is formed.