Question

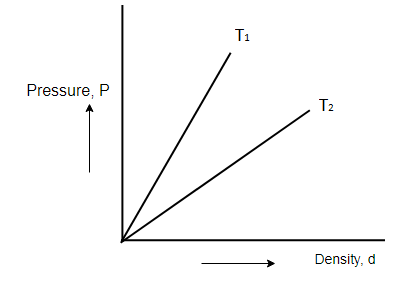
In Boyle's experiment for a given gas at different temperatures the graph drawn between pressure and density are straight lines as shown then:

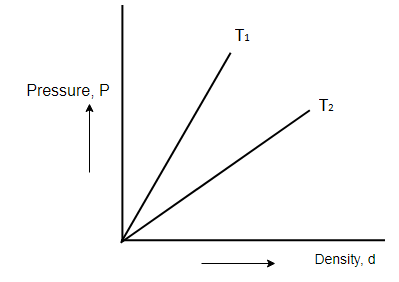
A. ${{T}_{1}}>{{T}_{2}}$
B. ${{T}_{2}}>{{T}_{1}}$
C. ${{T}_{1}}={{T}_{2}}$
D. ${{T}_{1}}^{3}={{T}_{2}}$

Answer 1

Pressure- density graph of a gas at different temperatures is given here. We have an ideal gas equation which relates pressure and temperature. And this equation can be converted in terms of pressure density and temperature.
Formula used:
$PV=nRT$
$\text{n=}\dfrac{m}{M}$
$d=\dfrac{m}{V}$
$\text{y=mx+c}$

Complete answer:

We have ideal gas law,
$PV=nRT$ --------- 1
Where,
$P=\text{Pressure of the gas}$
$\text{V= Volume of the gas}$
$\text{n= Number of moles of the gas}$
$\text{R=Gas constant}$
$\text{T= Temperature of the gas}$
Since the graph is drawn between pressure and density, let’s convert the ideal gas equation in terms of density and pressure.
We have,
Number of moles,
$\text{n=}\dfrac{m}{M}$
Where, $M-\text{Molar mass of the gas}$
$\text{m- mass of the gas}$
Then,
$PV=\dfrac{m}{M}RT$
$P=\dfrac{m}{M}\dfrac{RT}{V}$
We have, density, $d=\dfrac{m}{V}$
$P=\dfrac{dRT}{M}$
$P=dT\left( \dfrac{R}{M} \right)$ -------- 2
Here $R$and $M$ are constant. Now the ideal gas equation is converted in terms of $P,d\text{ and T}$
We have, straight line equation $\text{y=mx+c}$----- 3
Comparing the equation 2 with equation 3
$Slope=T\left( \dfrac{R}{M} \right)$
Since $\dfrac{R}{M}$ is constant, $T$ determines the slope of the Pressure-density graph.
i.e., as the value of $T$ increases, slope also increases.
From the graph, slope of ${{T}_{1}}$ is higher than slope of ${{T}_{2}}$
${{T}_{1}}\left( \dfrac{R}{M} \right)>{{T}_{2}}\left( \dfrac{R}{M} \right)$
Hence,
${{T}_{1}}>{{T}_{2}}$

So, the correct answer is “Option A”.

Note:
Ideal gas law can be used in problems in which gases are involved. Unless specified in the question, most of the ideal gas equations only work if S.I. units are used. i.e., while applying the ideal gas equation to solve the problems, convert the pressure in $Pascal(Pa)$, Volume in ${{m}^{3}}$ and temperature in$Kelvin(K)$. If we have $N-\text{ No}\text{. of molecules of gas}$ in the question, instead of $\text{n - no}\text{. of moles}$, we can use the ideal gas equation, $PV=N{{k}_{B}}T$ , Where, ${{\text{k}}_{\text{B}}}\text{(Boltzmann }\\!\\!'\\!\\!\text{ s constant) =}1.38\times {{10}^{-23}}\dfrac{J}{K}$