Question

In ${ BI }_{ 3 }$ molecule distance between two I atoms is found to be 3.54 $\overset { o }{ A }$. Also, ${ BI }_{ 3 }$ has ${ sp }^{ 2 }$-hybridised boron atom. If the radius of a covalently bonded I atom is 1.33, the covalent radius of boron will be X $\overset { o }{ A }$. Find the value of 100X.

Answer 1

Here we need to determine the shape of the molecule using VSEPR theory and hybridization theory and then use trigonometric functions in order to arrive at the answer.

Complete step by step solution:
In order to solve this question, we will use the VSEPR and hybridisation theory. In order to determine the hybridization of an atom in a molecule we should follow the following steps:
-First, you have to determine the Lewis structure of the molecule.
-Now assign the regions of electron density around the atom using VSEPR theory for predicting the shape of the molecule (single bonds, multiple bonds, radicals, and lone pairs each will count as one region).
-Now we can determine the set of hybridized orbitals corresponding to the geometry determined using VSEPR theory.
The Lewis structure of ${ BI }_{ 3 }$ is given below:

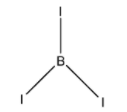
From the above structure, it is clear that the regions of electron density around the central atom are three. Therefore the geometry of the molecule is a Trigonal planar according to VSEPR theory. For a Trigonal planar molecule, the central atom must undergo ${ sp }^{ 2 }$ hybridization. The 2s and two 2p orbitals of Boron combine together in order to give three ${ sp }^{ 2 }$ hybrid orbitals.
Now it is given that the radius of the I atom is 1.33 $\overset { o }{ A }$. Let the bond length of the B-I bond be A. The radius of the B atom is X $\overset { o }{ A }$. The distance between two I atoms in the structure is 3.54 $\overset { o }{ A }$. The diagram is shown below:

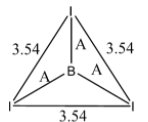
Taking one of the Isosceles triangles, we get:

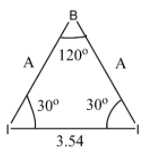
Now, we will draw a perpendicular line from B to the line connecting the two I atoms.

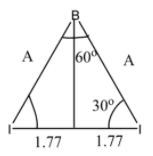
Let the length of the perpendicular be h, then
$\tan { { 30 }^{ o }=\dfrac { h }{ 1.77 } = } \dfrac { 1 }{ \sqrt { 3 } }$
$\Rightarrow h=1.02\overset { o }{ A }$
Now, applying Pythagoras theorem,
${ A }^{ 2 }=({ 1.02) }^{ 2 }+{ (1.77) }^{ 2 }$
${ \Rightarrow A=2.042 \overset { o }{ A } }$
This length is the sum of the radius of I and B, therefore
$2.42\overset { o }{ A } =1.33\overset { o }{ A } +X\overset { o }{ A }$
${ \Rightarrow X=0.712\overset { o }{ A } }$
So, ${ 100X=0.712\overset { o }{ A } \times 100=71.2 \overset { o }{ A } }$

Hence 100X is equal to $71.2\overset { o }{ A }$.

Note: Hybridization and VSEPR theory can only be applied when the molecules contain small central atoms. It cannot explain the structure of transition metal compounds since it does not concern itself with the inactive lone pairs and the sizes of the substituent groups.