Question

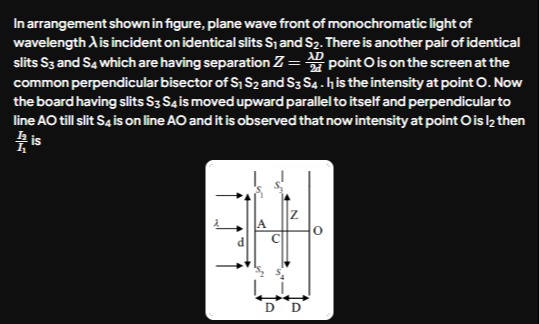
In arrangement shown in figure, plane wave front of monochromatic light of wavelength $\lambda$ is incident on identical slits $S_1$ and $S_2$. There is another pair of identical slits $S_3$ and $S_4$ which are having separation $Z = \frac{\lambda D}{2d}$ point O is on the screen at the common perpendicular bisector of $S_1 S_2$ and $S_3 S_4$. $I_1$ is the intensity at point O. Now the board having slits $S_3 S_4$ is moved upward parallel to itself and perpendicular to line AO till slit $S_4$ is on line AO and it is observed that now intensity at point O is $I_2$ then $\frac{I_2}{I_1}$ is

• A. 1/4

Answer 1

Answer: (A)

1/4

Answer 2

Initially, the four slits are arranged so that point O is equidistant from each slit. Thus the waves from $S_1$, $S_2$, $S_3$, and $S_4$ all arrive in-phase. If we assume each slit produces an amplitude A, the resultant amplitude is

$A_{total1} = A + A + A + A = 4A$

and hence,

$I_1 \propto (4A)^2 = 16A^2$.

When the board having $S_3$ and $S_4$ is moved upward (perpendicularly to AO) until $S_4$ lies along AO, the symmetry for that pair is lost. With the given condition $Z = \frac{\lambda D}{2d}$ the relative shift produces a phase difference of $\pi$ between $S_3$ and $S_4$ (i.e. they cancel each other). Thus, the net contribution from $S_3$ and $S_4$ becomes zero.

Now only $S_1$ and $S_2$ contribute, with

$A_{total2} = A + A = 2A$

and so,

$I_2 \propto (2A)^2 = 4A^2$.

Therefore,

$\frac{I_2}{I_1} = \frac{4A^2}{16A^2} = \frac{1}{4}$.