Question
Question: In ancient times, a weight thermometer was used to measure the temperature. The apparatus is shown i...
In ancient times, a weight thermometer was used to measure the temperature. The apparatus is shown in figure. The container's volume at absolute temperature is V0. γL is the coefficient of volume expansion of the liquid filled. γC is the coefficient of volume expansion of the metal of the container. Density of liquid at absolute temperature is ρL0. If △m is the mass of liquid overflowing, then △T is given by
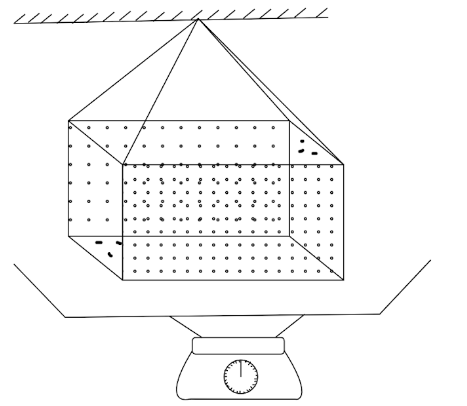
A. △T=ρL0V0γL−△mγL△m
B. △T=ρL0V0γL+△mγL△m
C. △T=ρL0V0(γL−γC)−△mγL△m
D. none of these
Solution
We will find out the volume of the liquid that will overflow when there is any temperature change. After that we simply know that change in mass is equal to the change in velocity of the substance to its density. Then, by ordinary calculation we will be able to find a change in temperature.
Formula used:
ρf(1+γ△T)=ρi
where f implies final ang i implies initial.
Also the formula for volume expansion is given as,
Vf=Vi(1+γ△T)
where, Vi is the final volume, Vi is the initial volume and γ is the coefficient of volume expansion.
Complete step by step answer:
In the above question it is mentioned that γL is the coefficient of volume expansion of the liquid filled. γC is the coefficient of volume expansion of the metal of the container. ρL0 is the density of the liquid at absolute temperature.
V0 is the volume of the container. We know that,
Vf=Vi(1+γ△T) where, Vi is the final volume, Vi is the initial volume and γ is the coefficient of volume expansion.
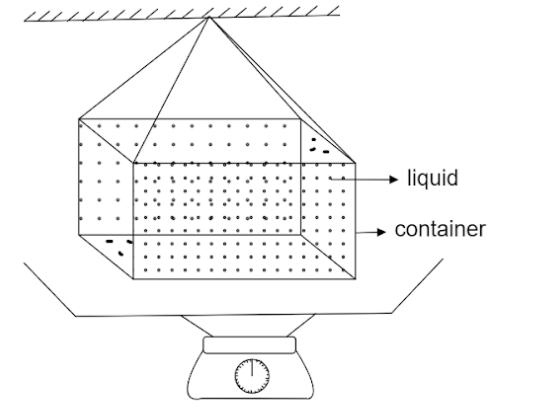
Thus from the above question we get,
{V_f} = {V_0}\left\\{ {1 + \left( {{\gamma _L} - {\gamma _C}} \right)\vartriangle T} \right\\}
⇒Vf−V0=V0(γL−γC)△T
Now, the change in volume is given as,
△V=V0(γL−γC)△T−−−−−(1)
Again we should find the change in density,
Let ρL be the final density after change of temperature △T,
ρL=(1+γL△T)ρL0−−−−−(2)
Now, the mass collected can be represented as,
△m=△V×ρL
Substituting the value of △V and ρL from equation (1) and (2) we get,
△m=V0(γL−γC)△T×(1+γL△T)ρL0
Interchanging the variables we get,
∴△T=ρL0V0(γL−γC)−△mγL△m
So, the correct option is C.
Note: There is a possibility to overlook the volumetric expansion of the liquid inside the container. It is most important to recall that the volumetric expansion of solids helps to expand the metal surface which in turn allows less liquid to overflow. It must be subtracted while finding the mass overflow as done in the solution.
