Question

In an oscillator, for sustained oscillations, Barkhausen criterion is $A\beta =?$( A is the voltage gain without feedback, $\beta$ is the feedback factor)
A) Zero
B) $\dfrac{1}{2}$
C) 1
D) 2

Answer 1

We need to find the relation between the voltage gain in an oscillation where there is no feedback and the feedback factor to solve this problem. The Barkhausen criterion also needs to be explained to understand the given situation.

Complete answer:
An amplifier is essentially an electronic device which utilises the feedback mechanism to convert the comparatively smaller input voltage signals to output signals of larger amplitude. For this process, the amplifier should be in an operational condition.

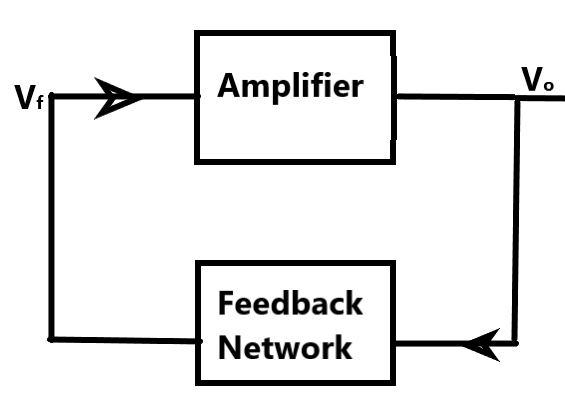
Barkhausen's condition is applicable to circuits which involve a feedback loop with positive feedback. It gives whether the given circuit can have an oscillating nature of the signal feedback will get distorted by the passage of time.
For the amplifier to have an oscillation, according to the Barkhausen criterion the product of the gain in the amplifier and the feedback factor must equal unity.
i.e.,
$\left| A\beta \right|=1$
In any other case, the oscillation will not persist in the circuit. If the product is less than one, then the loop gain will be lowering with each cycle and therefore, the oscillation fades away. On the other hand, if the product is greater than one, then the loop gain becomes unsteady and thus the oscillation becomes unpredictable.
Therefore, the Barkhausen condition requires the loop gain to be unity.
$\therefore \left| A\beta \right|=1$
This is the required solution.

The correct answer is option C.

Note:
The Barkhausen criterion is one of the basic criterions to be followed in the operational amplifiers with a positive feedback mechanism. This enables the maximum utilization of the available energy without any loss due to the oscillation involved.