Question

In an orthorhombic crystal, a lattice plane cuts intercepts in the ratio 1:2:3 along a,b and c axes. Find the miller indices of the plane. Sketch the plane and calculate the interplanar spacing, given that a=1A, b=2A and c=3A.

Answer 1

We have to calculate Miller indices by taking the reciprocals of intercepts and for calculating the interplanar spacing, we have to use the formula,
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{h^ + } + hk + {k^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{l^2}}}{{{c^2}}}} \right)$
Here, h, k, and l are miller indices.

Complete step by step answer:
We know that the orthorhombic crystal system is one of the 7 crystal systems.
Orthorhombic lattices comes from enlarging a cubic lattice along two of its orthogonal pairs by two factors, that leads in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are different.
The intersection of all three bases at 90° angles, so the three lattice vectors remain mutually orthogonal.
We know that Miller indices of a plane are the reciprocals of the intercepts of that corresponding to unit length.
Thus, intercepts are a:b:c=1:2:3.
So let us now take the reciprocals:
$\dfrac{1}{a}:\dfrac{1}{b}:\dfrac{1}{c} = \dfrac{1}{1}:\dfrac{1}{2}:\dfrac{1}{3}$
(or) We can take L.C.M and by taking L.C.M, we get the value of miller indices as 6,3,2.
The value of h is 6.
The value of k is 3.
The value of l is 2.
We can represent the miller indices as $\left( {hkl} \right) = \left( {632} \right)$
Let us now calculate the interplanar spacing for orthorhombic crystals.
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{h^ + } + hk + {k^2}}}{{{a^2}}}} \right) + \left( {\dfrac{{{l^2}}}{{{c^2}}}} \right)$
Let us now substitute the values of a, c, h, k, and l to calculate the interplanar spacing.
$\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{4}{3}\left( {\dfrac{{{{\left( 6 \right)}^2} + \left( 6 \right)\left( 2 \right) + {{\left( 2 \right)}^2}}}{{{{\left( 1 \right)}^2}}}} \right) + \left( {\dfrac{{{{\left( 2 \right)}^2}}}{{{{\left( 3 \right)}^2}}}} \right)$
$\Rightarrow$ $\dfrac{1}{{{d_{hkl}}^2}} = \dfrac{{760}}{9}$
$\Rightarrow$ ${d_{hkl}}^2 = \dfrac{9}{{760}}$
$\Rightarrow$ ${d_{hkl}} = \dfrac{3}{{\sqrt {760} }}$
The inter-planar spacing is $\dfrac{3}{{\sqrt {760} }}$.
The plane is sketched as,

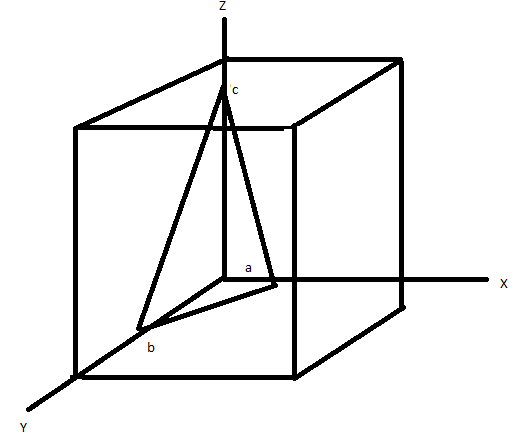
Note:
We have to know that in two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular. In three dimensions, primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic are the four orthorhombic Bravais lattices.